题目内容
已知椭圆C1和双曲线C2有公共焦点F1,F2,C1的离心率为e1,C2离心率为e2,p为C1与C2的一个公共点,且满足
+
=2,则
•
的值为( )
| 1 |
| e12 |
| 1 |
| e22 |
| PF1 |
| PF2 |
| A、-1 | B、0 | C、1 | D、2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设焦距为2c、椭圆的长轴长2a、双曲线的实轴长为2m,根据椭圆和双曲线的离心率和条件列出m,a,c的等式,再由椭圆、双曲线的定义列出关于|PF1|和|PF2|的方程,整理后由勾股定理和向量垂直的条件即可求值.
解答:
解:由题意设焦距为2c,椭圆的长轴长2a,双曲线的实轴长为2m,
所以e1=
,e2=
,代入
+
=2得,a2+m2=2c2,
不妨令P在双曲线的右支上,
由双曲线的定义|PF1|-|PF2|=2m ①
由椭圆的定义|PF1|+|PF2|=2a ②
则①2+②2得,|PF1|2+|PF2|2=2a2+2m2=4c2=|F1F2|2,
所以∠F1PF2=900,则
⊥
,即
•
=0,
故选:B.
所以e1=
| c |
| a |
| c |
| m |
| 1 |
| e12 |
| 1 |
| e22 |
不妨令P在双曲线的右支上,
由双曲线的定义|PF1|-|PF2|=2m ①
由椭圆的定义|PF1|+|PF2|=2a ②
则①2+②2得,|PF1|2+|PF2|2=2a2+2m2=4c2=|F1F2|2,
所以∠F1PF2=900,则
| PF1 |
| PF2 |
| PF1 |
| PF2 |
故选:B.
点评:本题考查椭圆、双曲线的定义以及离心率,勾弦定理,向量垂直的条件,解决本题的关键是根据条件灵活变形,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
“φ=2kπ+
,k∈Z”是“函数f(x)=cos(2x+φ)的图象过原点”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
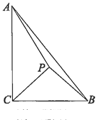 如图,在Rt△ABC中,∠ACB=
如图,在Rt△ABC中,∠ACB=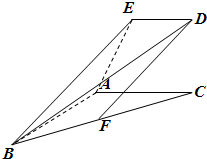 如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.
如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.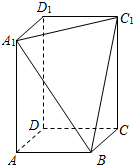 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.