题目内容
设等差数列{an}的前n项和为Sn,若a2=-11,a5+a9=-2,则当Sn取最小值时,n等于( )
| A、9 | B、8 | C、7 | D、6 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知求出等差数列的首项和公差,写出通项公式,由通项小于等于0求得n的值得答案.
解答:
解:设等差数列的首项为a1,公差为d,
由a2=-11,a5+a9=-2,得
,解得:
.
∴an=-15+2n.
由an=-15+2n≤0,解得:n≤
.
∴当Sn取最小值时,n等于7.
故选:C.
由a2=-11,a5+a9=-2,得
|
|
∴an=-15+2n.
由an=-15+2n≤0,解得:n≤
| 15 |
| 2 |
∴当Sn取最小值时,n等于7.
故选:C.
点评:本题考查了等差数列的通项公式,考查了等差数列的前n项和,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,设全集U=R,M={x|x>2},N={0,1,2,3},则图中阴影部分所表示的集合是( )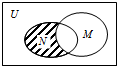

| A、{3} |
| B、{0,1} |
| C、{0,1,2} |
| D、{0,1,2,3} |
已知复数z=(1-sinθ)+icosθ(θ∈[
,π]),则|z|等于( )
| π |
| 2 |
A、cos
| ||||||
B、sin
| ||||||
C、
| ||||||
D、
|
 已知函数f(x)=Asin(ωx-
已知函数f(x)=Asin(ωx-| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
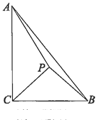 如图,在Rt△ABC中,∠ACB=
如图,在Rt△ABC中,∠ACB=