题目内容
已知m∈R,复数z=
+(m2+2m-1)i,当m为何值时,
(1)z∈R
(2)z是虚数
(3)z是纯虚数.
| m(m+2) |
| m-1 |
(1)z∈R
(2)z是虚数
(3)z是纯虚数.
考点:复数的基本概念
专题:数系的扩充和复数
分析:(1)当m满足
时,解得即可.
(2)由
,解得即可.
(3)由
,解得即可.
|
(2)由
|
(3)由
|
解答:
解:(1)当m满足
时,解得m=-1±
,∴m=-1±
,z为实数.
(2)由
,解得m≠1,且m≠-1±
,∴m≠1,且m≠-1±
,z为虚数.
(3)由
,解得m=0或-2时,∴m=0或-2时,z是纯虚数.
|
| 2 |
| 2 |
(2)由
|
| 2 |
| 2 |
(3)由
|
点评:本题考查了复数复数为实数、虚数、纯虚数的充要条件,考查了计算能力,属于基础题.

练习册系列答案
相关题目
如图,设全集U=R,M={x|x>2},N={0,1,2,3},则图中阴影部分所表示的集合是( )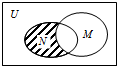

| A、{3} |
| B、{0,1} |
| C、{0,1,2} |
| D、{0,1,2,3} |
已知复数z=(1-sinθ)+icosθ(θ∈[
,π]),则|z|等于( )
| π |
| 2 |
A、cos
| ||||||
B、sin
| ||||||
C、
| ||||||
D、
|
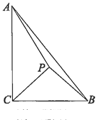 如图,在Rt△ABC中,∠ACB=
如图,在Rt△ABC中,∠ACB=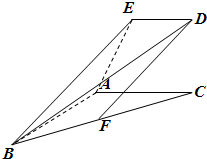 如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.
如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.