题目内容
已知函数f(x)=lnx+ax2+bx(其中a、b为常数且a≠0)在x=1处取得极值.
(1)当a=1时,求f(x)的极大值点和极小值点;
(2)若f(x)在(0,e]上的最大值为1,求a的值.
(1)当a=1时,求f(x)的极大值点和极小值点;
(2)若f(x)在(0,e]上的最大值为1,求a的值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)通过求解函数的导数,结合函数的极值点,求出b,然后通过函数的单调性求解极值点即可.
(2)通过f′(x)=0求出x1=1,x2=
,然后讨论当
<0时,f(x)在区间(0,e]上的最大值为f(1),求出a.(ⅱ)当a>0时,①当
<1时,利用f(x)在(0,
)上单调递增,(
,1)上单调递减,(1,e)上单调递增,求出a=
.②当1≤
<e时,f(x)在区间(0,1)上单调递增,(1,
)上单调递减,(
,e)上单调递增,求解a即可.③当x2=
≥e时,f(x)在区间(0,1)上单调递增,在(1,e)上单调递减,求解a即可.
(2)通过f′(x)=0求出x1=1,x2=
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| e-2 |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
解答:
(本小题满分12分)
解:(1)因为f(x)=lnx+ax2+bx,所以f′(x)=
+2ax+b.
因为函数f(x)=lnx+ax2+bx在x=1处取得极值,
f′(1)=1+2a+b=0.当a=1时,b=-3,f′(x)=
,
f′(x)、f(x)随x的变化情况如下表:
所以f(x)的单调递增区间为(0,
)和(1,+∞),单调递减区间为(
,1)----(3分)
所以f(x)的极大值点为
,f(x)的极小值点为1.---------------(4分)
(2)因为f′(x)=
=
(x>0),
令f′(x)=0得,x1=1,x2=
,
因为f(x)在x=1处取得极值,所以x2=
≠x1=1,
(ⅰ)当
<0时,f(x)在(0,1)上单调递增,在(1,e]上单调递减,
所以f(x)在区间(0,e]上的最大值为f(1),令f(1)=1,解得a=-2,--------(7分)
(ⅱ)当a>0时,x2=
>0,
①当
<1时,f(x)在(0,
)上单调递增,(
,1)上单调递减,(1,e)上单调递增,
所以最大值1可能在x=
或x=e处取得,
而f(
)=ln
+a(
)2-(2a+1)•
=ln
-
-1<0,
所以f(e)=lne+ae2-(2a+1)e=1,解得a=
;------------------(9分)
②当1≤
<e时,f(x)在区间(0,1)上单调递增,(1,
)上单调递减,(
,e)上单调递增,
所以最大值1可能在x=1或x=e处取得,而f(1)=ln1+a-(2a+1)<0,
所以f(e)=lne+ae2-(2a+1)e=1,
解得a=
,与1<x2=
<e矛盾;
③当x2=
≥e时,f(x)在区间(0,1)上单调递增,在(1,e)上单调递减,
所以最大值1可能在x=1处取得,而f(1)=ln1+a-(2a+1)<0,矛盾.
综上所述,a=
或a=-2.------------------------(12分)
解:(1)因为f(x)=lnx+ax2+bx,所以f′(x)=
| 1 |
| x |
因为函数f(x)=lnx+ax2+bx在x=1处取得极值,
f′(1)=1+2a+b=0.当a=1时,b=-3,f′(x)=
| 2x2-3x+1 |
| x |
f′(x)、f(x)随x的变化情况如下表:
| x | (0,
|
| (
| 1 | (1,+∞) | ||||||
| f′(x) | + | 0 | - | 0 | + | ||||||
| f(x) | ?增函数 | 极大值 | ?减函数 | 极小值 | ?增函数 |
| 1 |
| 2 |
| 1 |
| 2 |
所以f(x)的极大值点为
| 1 |
| 2 |
(2)因为f′(x)=
| 2ax2-(2a+1)x+1 |
| x |
| (2ax-1)(x-1) |
| x |
令f′(x)=0得,x1=1,x2=
| 1 |
| 2a |
因为f(x)在x=1处取得极值,所以x2=
| 1 |
| 2a |
(ⅰ)当
| 1 |
| 2a |
所以f(x)在区间(0,e]上的最大值为f(1),令f(1)=1,解得a=-2,--------(7分)
(ⅱ)当a>0时,x2=
| 1 |
| 2a |
①当
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
所以最大值1可能在x=
| 1 |
| 2a |
而f(
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 4a |
所以f(e)=lne+ae2-(2a+1)e=1,解得a=
| 1 |
| e-2 |
②当1≤
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
所以最大值1可能在x=1或x=e处取得,而f(1)=ln1+a-(2a+1)<0,
所以f(e)=lne+ae2-(2a+1)e=1,
解得a=
| 1 |
| e-2 |
| 1 |
| 2a |
③当x2=
| 1 |
| 2a |
所以最大值1可能在x=1处取得,而f(1)=ln1+a-(2a+1)<0,矛盾.
综上所述,a=
| 1 |
| e-2 |
点评:考查导数的基本概念(极值点的概念)、应用,含字母的分类讨论的思想.考查分析问题解决问题的能力.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
若复数
(i为虚数単位)是纯虚数,则实数 a的值为( )
| 1+ai |
| 2+i |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
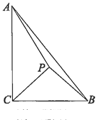 如图,在Rt△ABC中,∠ACB=
如图,在Rt△ABC中,∠ACB=