题目内容
设集合 M={-l，0，l，2}，N={y|y=2x+1，x∈R}，则M∩N= ．
考点：交集及其运算
专题：集合
分析：由指数函数的性质求出集合N，再由交集的运算求出M∩N．
解答：
解：由y=2x+1＞1得，N={y|y＞1}，
又集合M={-l，0，l，2}，则M∩N={2}，
故答案为：{2}．
又集合M={-l，0，l，2}，则M∩N={2}，
故答案为：{2}．
点评：本题考查交集及其运算，以及指数函数的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
下列命题正确的是（ ）
| A、?x∈R，都有x2-3x+3＞0成立 |
| B、?x0∈R，使sin2x0+cos2x0＜1成立 |
| C、“?x0∈R，使x02-1＜0”的否定是“?x∈R，都有x2-1＞0” |
| D、若“p∨q”为假，则命题p、q中一个真另一个假 |
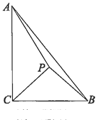如图，在Rt△ABC中，∠ACB=