题目内容
已知偶函数f(x)在[0,+∞)单调递减,且f(-2)=0,若f(x-2)>0,则x的取值范围是 .
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系将不等式等价转化为f(|x-2|)>f(2),即可得到结论.
解答:
解:∵偶函数f(x)在[0,+∞)单调递减,f(-2)=0,
∴f(-2)=f(2)=0,
∴不等式f(x-,2)>0等价为f(x-2)>f(2),
即f(|x-2|)>f(2),
∴|x-2|<2,
解得0<x<4,
故答案为:(0,4)
∴f(-2)=f(2)=0,
∴不等式f(x-,2)>0等价为f(x-2)>f(2),
即f(|x-2|)>f(2),
∴|x-2|<2,
解得0<x<4,
故答案为:(0,4)
点评:本题主要考查函数奇偶性和单调性之间的关系的应用,将不等式等价转化为f(|x-2|)>f(2)是解决本题的关键.

练习册系列答案
相关题目
已知复数z=(1-sinθ)+icosθ(θ∈[
,π]),则|z|等于( )
| π |
| 2 |
A、cos
| ||||||
B、sin
| ||||||
C、
| ||||||
D、
|
“φ=2kπ+
,k∈Z”是“函数f(x)=cos(2x+φ)的图象过原点”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
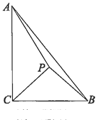 如图,在Rt△ABC中,∠ACB=
如图,在Rt△ABC中,∠ACB=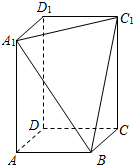 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.