题目内容
已知数列{an}满足a2=5,且其前n项和Sn=pn2-n.
(Ⅰ)求p的值和数列{an}的通项公式;
(Ⅱ)设数列{bn}为等比数列,公比为p,且其前n项和Tn满足T5<S5,求b1的取值范围.
(Ⅰ)求p的值和数列{an}的通项公式;
(Ⅱ)设数列{bn}为等比数列,公比为p,且其前n项和Tn满足T5<S5,求b1的取值范围.
考点:等比数列的性质,数列的求和
专题:综合题,等差数列与等比数列
分析:(Ⅰ)由题意,得S1=p-1,S2=4p-2,利用a2=5,S2=a1+a2,可得S2=4p-2=p-1+5,即可求p的值;再写一式,两式相减,即可求出数列{an}的通项公式;
(Ⅱ)求出Tn,利用T5<S5,建立不等式,即可求b1的取值范围.
(Ⅱ)求出Tn,利用T5<S5,建立不等式,即可求b1的取值范围.
解答:
解:(Ⅰ)由题意,得S1=p-1,S2=4p-2,
因为 a2=5,S2=a1+a2,
所以 S2=4p-2=p-1+5,
解得 p=2.…(3分)
所以 Sn=2n2-n.
当n≥2时,由an=Sn-Sn-1,…(5分)
得 an=(2n2-n)-[2(n-1)2-(n-1)]=4n-3.…(7分)
验证知n=1时,a1符合上式,
所以an=4n-3,n∈N*.…(8分)
(Ⅱ)由(Ⅰ),得Tn=
=b1(2n-1).…(10分)
因为 T5<S5,
所以 b1(25-1)<2×52-5,
解得 b1<
. …(12分)
又因为b1≠0,
所以b1的取值范围是(-∞,0)∪(0,
). …(13分)
因为 a2=5,S2=a1+a2,
所以 S2=4p-2=p-1+5,
解得 p=2.…(3分)
所以 Sn=2n2-n.
当n≥2时,由an=Sn-Sn-1,…(5分)
得 an=(2n2-n)-[2(n-1)2-(n-1)]=4n-3.…(7分)
验证知n=1时,a1符合上式,
所以an=4n-3,n∈N*.…(8分)
(Ⅱ)由(Ⅰ),得Tn=
| b1(1-2n) |
| 1-2 |
因为 T5<S5,
所以 b1(25-1)<2×52-5,
解得 b1<
| 45 |
| 31 |
又因为b1≠0,
所以b1的取值范围是(-∞,0)∪(0,
| 45 |
| 31 |
点评:本题考查数列的性质和综合应用,考查数列的通项与求和,确定数列的通项是关键.

练习册系列答案
相关题目
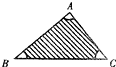 △ABC中,AB=8,AC=6,BC=10,顶点A、B、C处分别有一枚半径为1的硬币(顶点A、B、C分别与硬币的中心重合).向△ABC内部投一点,那么该点落在阴影部分的概率为( )
△ABC中,AB=8,AC=6,BC=10,顶点A、B、C处分别有一枚半径为1的硬币(顶点A、B、C分别与硬币的中心重合).向△ABC内部投一点,那么该点落在阴影部分的概率为( )A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
当x∈[0,π]时,函数f(x)=cosx-
sinx的值域是( )
| 3 |
| A、[-2,1] | ||
| B、[-1,2] | ||
| C、[-1,1] | ||
D、[-2,
|
已知全集U=R,集合A={x|x+1>0},B={x|y=loga(x+2)},则集合(∁UA)∩B=( )
| A、(-2,-1) |
| B、(-2,-1] |
| C、(-∞,-2) |
| D、(-1,-∞) |
已知α是第二象限角,且sin(
+α)=-
,则tan2α的值为( )
| π |
| 2 |
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知F1,F2分别是双曲线
-
=1的左、右焦点,P为双曲线右支上的任意一点,则
的最小值为( )
| x2 |
| 4 |
| y2 |
| 21 |
| |PF1|2 |
| |PF2| |
| A、24 | B、20 | C、16 | D、12 |
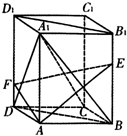 如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.