题目内容
3.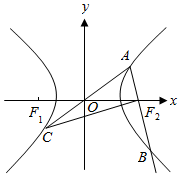 如图,点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左右焦点,点A、B、C分别为双曲线上三个不同的点,且AC经过坐标原点O,并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$,$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左右焦点,点A、B、C分别为双曲线上三个不同的点,且AC经过坐标原点O,并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$,$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
分析 令|AF2|=m,则|BF2|=2m,|AB|=3m,由题意可得四边形AF1CF2为矩形,运用直角三角形的勾股定理和双曲线的定义,可得a,c的关系,运用离心率公式计算即可得到所求值.
解答 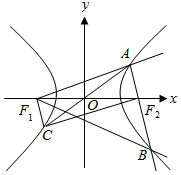 解:令|AF2|=m,则|BF2|=2m,|AB|=3m,
解:令|AF2|=m,则|BF2|=2m,|AB|=3m,
由$\overrightarrow{CO}=\overrightarrow{OA}$及$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,
可得,四边形AF1CF2为矩形,
所以有$\left\{\begin{array}{l}|A{F_1}|=2a+m\\|B{F_1}|=2a+2m\end{array}\right.$,
而在Rt△AF1B中,(2a+m)2+(3m)2=(2a+2m)2,
化简可得:$m=\frac{2}{3}a$,
故有$|A{F_1}|=\frac{8}{3}a$,$|A{F_2}|=\frac{2}{3}a$,
即$4{c^2}={(\frac{8}{3}a)^2}+{(\frac{2}{3}a)^2}$,
化简可得:$c=\frac{{\sqrt{17}}}{3}a$,
即$e=\frac{{\sqrt{17}}}{3}$.
故答案为:$\frac{\sqrt{17}}{3}$.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的定义和勾股定理,考查化简整理的运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1的一个焦点在抛物线y2=8x的准线上,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
14.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点到一条渐近线的距离等于焦距的$\frac{1}{4}$,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{3}}{3}$ |
8.以双曲线$\frac{{x}^{2}}{3}$-y2=1的左右焦点为焦点,离心率为$\frac{1}{2}$的椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | D. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{12}$=1 |
15.已知直线y=1-x与双曲线ax2+by2=1(a>0,b<0)的渐近线交于A,B两点,且过原点和线段AB中点的直线的斜率为$-\frac{{\sqrt{3}}}{2}$,则$\frac{a}{b}$的值为( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{2\sqrt{3}}}{3}$ | C. | $-\frac{{9\sqrt{3}}}{2}$ | D. | $-\frac{{2\sqrt{3}}}{27}$ |
12.已知实数x,y满足条件$\left\{\begin{array}{l}y≤x\\ x+y≥2\\ 2x+y≥6\end{array}\right.$,则z=3x+2y的取值范围是( )
| A. | (-∞,10] | B. | [5,10] | C. | [8,+∞) | D. | [8,10] |
13.设不等式组$\left\{\begin{array}{l}{x-y+4≥0}\\{x+y≥0}\\{x≤1}\end{array}\right.$表示的平面区域为Ω1,不等式组$\left\{\begin{array}{l}{-2≤x≤1}\\{-1≤y≤5}\end{array}\right.$表示的平面区域为Ω2,在区域Ω2内随机取一点,则该点是取自于区域Ω1的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |