题目内容
11.已知等差数列{an}的公差d=1,记{an}的前n项和为Sn,且满足S3+S5=S6.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设${b_n}={2^{a_n}}$,求使得bk+bk+1+bk+2+…+b2k-1=240的正整数k的值.
分析 (Ⅰ)等差数列{an}的公差d=1,an=a1+(n+1)d,S3+S5=S6,(3a1+3d)+(5a1+10d)=6a1+15d,求得a1=1,求得an=n;
(Ⅱ)写出${b}_{n}={2}^{n}$,将bk+bk+1+bk+2+…+b2k-1转化为22k-2k=240,求得2k=16,求得的值.
解答 解(Ⅰ)等差数列{an}的公差d=1,记{an}的前n项和为Sn,
∵S3+S5=S6,
(3a1+3d)+(5a1+10d)=6a1+15d,
解得:a1=d=1,
∴an=a1+(n+1)d=n,
(Ⅱ)${b}_{n}={2}^{n}$,
bk+bk+1+bk+2+…+b2k-1=2k+2k+1+2k+2+22k-1=22k-2k,
令t=2k>0,则t2-t=240,解得:t=16,t=-15,
∴2k=16,
∴k=4.
点评 题主要考查数列通项公式和前n项和的求解,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,c是半焦轴距,P是双曲线上异于顶点的点,满足ctan∠PF1F2=atan∠PF2F1,则双曲线的离心率e的取值范围是( )
| A. | (1,1+$\sqrt{2}$) | B. | ($\sqrt{2}$,1+$\sqrt{2}$) | C. | (1+$\sqrt{2}$,1+$\sqrt{3}$) | D. | (1+$\sqrt{2}$,+∞) |
1.如果执行如图所示的程序框图,那么输出的a=( )


| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 以上都不正确 |
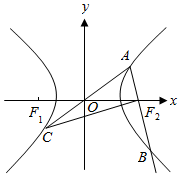 如图,点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左右焦点,点A、B、C分别为双曲线上三个不同的点,且AC经过坐标原点O,并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$,$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左右焦点,点A、B、C分别为双曲线上三个不同的点,且AC经过坐标原点O,并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$,$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.