题目内容
13.若二次函数f(x)=x2+bx+c满足f(0)=f(-2),且f(1)=3.(1)求f(x)的解析式;
(2)若在区间[-1,1]上,不等式f(x)>x+m恒成立,求实数m的取值范围.
分析 (1)根据所给条件,待定系数法求解b与c;
(2)据上一问的结果,将原不等式整理为m<g(x)恒成立,当x∈[-1,1],所以转化为求函数g(x)在给定区间的最小值问题.
解答 解:(1)由f(0)=f(-2),
则c=4-2b+c,即b=2.再有f(1)=3=1+b+c,则c=0,
故f(x)=x2+2x;
(2)由f(x)>x+m恒成立,则x2+2x>x+m;
∴x2+x>m,
令g(x)=x2+x,故g(x)在区间[-1,1]上的最小值为g(-$\frac{1}{2}$)=-$\frac{1}{4}$,
∴m<-$\frac{1}{4}$.
点评 1.待定系数求函数的解析式;2.二次函数求最值和恒成立问题的转化.

练习册系列答案
相关题目
1.若抛物线C1:y=$\frac{1}{4}$x2的焦点F到双曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的距离为$\frac{\sqrt{3}}{2}$,抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=-1的距离之和的最小时为$\sqrt{5}$,则双曲线C2的方程为( )
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
18.某校高三年级共1500人,在某次数学测验后分析学生试卷情况,需从中抽取一个容量为500的样本,按分层抽样,120分以上抽取100人,90~120分抽取250人,则该次测验中90分以下的人数是( )
| A. | 600 | B. | 450 | C. | 300 | D. | 150 |
5.信息时代,学生广泛使用手机,从某校学生中随机抽取200名,这200名学生中上课时间和不上时间都不使用手机的共有37人,这200名学生每天在校使用手机情况如下表:
利用以上数据,将统计的频率视为概率.
(1)求上表中m、n的值;
(2)求该校学生上课时间使用手机的概率.
| 分类 人数(人) 时间 | 一小时以上 | 一小时以内 | 不使用 | 合计 |
| 上课时间 | 23 | 55 | m | 98 |
| 不上课时间 | 17 | 68 | 17 | 102 |
| 合计 | 40 | 123 | n | 200 |
(1)求上表中m、n的值;
(2)求该校学生上课时间使用手机的概率.
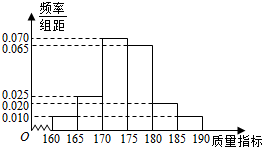 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.