题目内容
3.已知二次函数f(x)=x2-2x-1.(1)判断f(x)图象的开口方向、对称轴及单调性.
(2)解方程f(x)=x-3.
(3)当x∈[-1,2]时,求函数f(x)的最大值与最小值.
分析 (1)直接利用二次函数的性质写出结果即可.
(2)利用二次方程转化求解即可.
(3)求出函数的对称轴,以及二次函数的开口方向,求解闭区间上的最值.
解答 解:(1)二次函数f(x)=x2-2x-1.f(x)图象的开口向上、对称轴x=1,
f(x)在(-∞,1)内单调递减,f(x)在(1,+∞)内单调递增
(2)方程f(x)=x-3,即x2-2x-1=x-3,x2-3x+2=0,
(x-1)(x-2)=0,
解得x=1或x=2.
(3)二次函数f(x)=x2-2x-1.f(x)图象的开口向上、对称轴x=1,
f(x)min=f(1)=-2,
f(x)max=f(-1)=2.
点评 本题考查二次函数的简单性质的应用,二次函数闭区间上的最值的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.点A(a,1)在椭圆$\frac{x^2}{4}$+$\frac{y^2}{2}$=1的内部,则a的取值范围是( )
| A. | $(-\sqrt{2},\sqrt{2})$ | B. | $(-∞,-\sqrt{2})∪(\sqrt{2},+∞)$ | C. | (-2,2) | D. | (-1,1) |
14.双曲线的方程是$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1,点P在双曲线上,且|PF1|•|PF2|=36.则△F1PF2的面积是9$\sqrt{3}$.
11.已知函数$f(x)=\left\{\begin{array}{l}x+4,-3≤x≤0\\{x^2}-2x,0<x<4\\-x+2,4≤x≤5\end{array}\right.$,则f[f(f(2))]=( )
| A. | 2 | B. | -2 | C. | 4 | D. | 0 |
8.执行如图所示的程序框图,输出$s=\frac{2015}{2016}$.那么判断框内应填( )
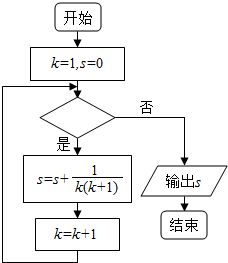

| A. | k≤2015 | B. | k≤2016 | C. | k≥2015 | D. | k≥2016 |
15.已知ABC中,A=30°,B=45°,b=$\sqrt{2}$,则a=( )
| A. | 3 | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
12.某市一高中二年级在期中考试后进行了研学活动,旅行社推出6条研学路线--A:历史,B:人文,C:诗歌,D:科技,E:政风,F:探秘.
(Ⅰ)假设每条线路被选中的可能性相同,若从上述6条线路中随机选择4条线路进行研学.求历史与科技两条线路都被选中的概率;
(Ⅱ)研学结束后,学校从参加研学的所有学生中,随机抽取了100名学生参加对本次研学满意度的调查,满意度得分的统计结果如下表:
试估算学生对本次研学满意度的平均得分.
(Ⅰ)假设每条线路被选中的可能性相同,若从上述6条线路中随机选择4条线路进行研学.求历史与科技两条线路都被选中的概率;
(Ⅱ)研学结束后,学校从参加研学的所有学生中,随机抽取了100名学生参加对本次研学满意度的调查,满意度得分的统计结果如下表:
| 满意度得分 | [0,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | 0 | 2 | 9 | 26 | 52 | 11 |