题目内容
4.设log23=t,s=log672,若用含t的式子表示s,则s=$\frac{3+2t}{1+t}$.分析 利用换底公式以及导数的运算法则化简S,然后求出结果.
解答 解:log23=t,s=log672=$\frac{{log}_{2}72}{{log}_{2}6}$=$\frac{3+2{log}_{2}3}{{1+log}_{2}3}$=$\frac{3+2t}{1+t}$.
故答案为:$\frac{3+2t}{1+t}$.
点评 本题考查对数的运算法则的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.双曲线的方程是$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1,点P在双曲线上,且|PF1|•|PF2|=36.则△F1PF2的面积是9$\sqrt{3}$.
15.已知ABC中,A=30°,B=45°,b=$\sqrt{2}$,则a=( )
| A. | 3 | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
12.某市一高中二年级在期中考试后进行了研学活动,旅行社推出6条研学路线--A:历史,B:人文,C:诗歌,D:科技,E:政风,F:探秘.
(Ⅰ)假设每条线路被选中的可能性相同,若从上述6条线路中随机选择4条线路进行研学.求历史与科技两条线路都被选中的概率;
(Ⅱ)研学结束后,学校从参加研学的所有学生中,随机抽取了100名学生参加对本次研学满意度的调查,满意度得分的统计结果如下表:
试估算学生对本次研学满意度的平均得分.
(Ⅰ)假设每条线路被选中的可能性相同,若从上述6条线路中随机选择4条线路进行研学.求历史与科技两条线路都被选中的概率;
(Ⅱ)研学结束后,学校从参加研学的所有学生中,随机抽取了100名学生参加对本次研学满意度的调查,满意度得分的统计结果如下表:
| 满意度得分 | [0,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | 0 | 2 | 9 | 26 | 52 | 11 |
9. 给出以下命题:
给出以下命题:
(1)函数f(x)=$\sqrt{{x}^{2}}$与函数g(x)=|x|是同一个函数;
(2)函数f(x)=ax+1(a>0且a≠1)的图象恒过定点(0,1);
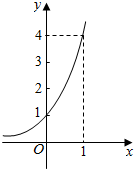
(3)设指数函数f(x)的图象如图所示,若关于x的方程f(x)=$\frac{m-1}{m+1}$有负数根,则实数m的取值范围是(1,+∞);
(4)若f(x)=$\left\{\begin{array}{l}{{2}^{x}+t(x≥0)}\\{g(x)(x<0)}\end{array}\right.$为奇函数,则f(f(-2))=-7;
(5)设集合M={m|函数f(x)=x2-mx+2m的零点为整数,m∈R},则M的所有元素之和为15.
其中所有正确命题的序号为( )
 给出以下命题:
给出以下命题:(1)函数f(x)=$\sqrt{{x}^{2}}$与函数g(x)=|x|是同一个函数;
(2)函数f(x)=ax+1(a>0且a≠1)的图象恒过定点(0,1);
(3)设指数函数f(x)的图象如图所示,若关于x的方程f(x)=$\frac{m-1}{m+1}$有负数根,则实数m的取值范围是(1,+∞);
(4)若f(x)=$\left\{\begin{array}{l}{{2}^{x}+t(x≥0)}\\{g(x)(x<0)}\end{array}\right.$为奇函数,则f(f(-2))=-7;
(5)设集合M={m|函数f(x)=x2-mx+2m的零点为整数,m∈R},则M的所有元素之和为15.
其中所有正确命题的序号为( )
| A. | (1)(2)(3) | B. | (1)(3)(5) | C. | (2)(4)(5) | D. | (1)(3)(4) |
16.将函数y=cos2x的图象向右平移φ个单位得到函数y=cos2x-$\sqrt{3}$sin2x的图象,则φ的一个可能取值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
14.若a,b,c∈R,则下列结论中正确的是( )
| A. | 若a>b,则a2>b2 | B. | 若a>b,则ac2>bc2 | C. | 若ac>bc,则a>b | D. | 若a>b,则a-c>b-c |