题目内容
已知椭圆的两个焦点坐标分别是(-
,0),(
,0),并且经过点(
,
).
(1)求椭圆的标准方程;
(2)若斜率为k的直线l经过点(0,-2),且与椭圆交于不同的两点A、B,求△OAB面积的最大值.
| 2 |
| 2 |
| ||
| 2 |
| ||
| 6 |
(1)求椭圆的标准方程;
(2)若斜率为k的直线l经过点(0,-2),且与椭圆交于不同的两点A、B,求△OAB面积的最大值.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)利用待定系数法求椭圆的标准方程,在求a时利用椭圆的定义比较简单;
(2)利用弦长公式先求出|AB|,然后利用面积公式构建关于斜率k的函数,通过换元法利用基本不等求△OAB面积的最大值.
(2)利用弦长公式先求出|AB|,然后利用面积公式构建关于斜率k的函数,通过换元法利用基本不等求△OAB面积的最大值.
解答:
解:(1)设椭圆的标准方程为
+
=1(a>b>0),
由椭圆的定义可得2a=
+
=2
.
∴a=
,又c=
,
∴b=1,
故椭圆的标准方程为
+y2=1.
(2)设直线l的方程为y=kx-2,
由
,得(1+3k2)x2-12kx+9=0,
依题意△=36k2-36>0,
∴k2>1(*)
设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
,
∴|AB|=
|x1-x2|=
×
,
由点到直线的距离公式得d=
,
∴S△=
×
×
×
=
.
设
=t(t>0),则k2=t2+1,
∴S△OAB=6×
=6×
=6×
≤
,
当且仅当t=
时,上式取等号,
所以,△OAB面积的最大值为
.
| x2 |
| a2 |
| y2 |
| b2 |
由椭圆的定义可得2a=
(
|
(
|
| 3 |
∴a=
| 3 |
| 2 |
∴b=1,
故椭圆的标准方程为
| x2 |
| 3 |
(2)设直线l的方程为y=kx-2,
由
|
依题意△=36k2-36>0,
∴k2>1(*)
设A(x1,y1),B(x2,y2),
则x1+x2=
| 12k |
| 1+3k2 |
| 9 |
| 1+3k2 |
∴|AB|=
| 1+k2 |
| 1+k2 |
6
| ||
| 1+3k2 |
由点到直线的距离公式得d=
| 2 | ||
|
∴S△=
| 1 |
| 2 |
| 1+k2 |
6
| ||
| 1+3k2 |
| 2 | ||
|
6
| ||
| 1+3k2 |
设
| k2-1 |
∴S△OAB=6×
| t |
| 1+3(t2+1) |
| t |
| 3t2+4 |
| 1 | ||
3t+
|
| ||
| 2 |
当且仅当t=
2
| ||
| 3 |
所以,△OAB面积的最大值为
| ||
| 2 |
点评:第(1)问用待定系数法求椭圆的方程时,也可以把点代入方程求解,但这种方法计算量大;第(2)问得到的面积表达式比较复杂,当函数表达式比较复杂时,考虑用换元法转化成简单函数,但要注意转化后函数的定义域.

练习册系列答案
相关题目
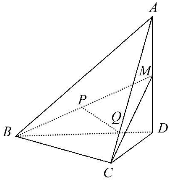 如图,四面体A-BCD中,AD⊥面BCD,BC⊥CD,AD=2,BD=2
如图,四面体A-BCD中,AD⊥面BCD,BC⊥CD,AD=2,BD=2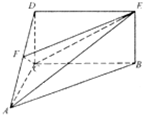 如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=
如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=