题目内容
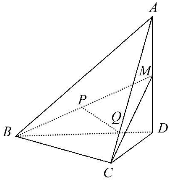 如图,四面体A-BCD中,AD⊥面BCD,BC⊥CD,AD=2,BD=2
如图,四面体A-BCD中,AD⊥面BCD,BC⊥CD,AD=2,BD=2| 2 |
| AC |
| QC |
(Ⅰ)证明:PQ∥平面BCD;
(Ⅱ)若二面角C-BM-D的大小为60°,求四面体A-BCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)取BD的中点O,在线段CD上取点F,使得DF=3CF,连接OP、OF、FQ.根据平行线分线段成比例定理结合三角形的中位线定理证出四边形OPQF是平行四边形,从而PQ∥OF,再由线面平行判定定理,证出PQ∥平面BCD;
(Ⅱ)过点C作CG⊥BD,垂足为G,过G作GH⊥BM于H,连接CH.根据线面垂直的判定与性质证出BM⊥CH,因此∠CHG是二面角C-BM-D的平面角,可得∠CHG=60°.设∠BDC=θ,用解直角三角形的方法算出HG和CG关于θ的表达式,最后在Rt△CHG中,根据正切的定义得出tan∠CHG,从而得到tanθ,由此可得∠BDC,进而可求四面体A-BCD的体积.
(Ⅱ)过点C作CG⊥BD,垂足为G,过G作GH⊥BM于H,连接CH.根据线面垂直的判定与性质证出BM⊥CH,因此∠CHG是二面角C-BM-D的平面角,可得∠CHG=60°.设∠BDC=θ,用解直角三角形的方法算出HG和CG关于θ的表达式,最后在Rt△CHG中,根据正切的定义得出tan∠CHG,从而得到tanθ,由此可得∠BDC,进而可求四面体A-BCD的体积.
解答:
解:(Ⅰ)取BD的中点O,在线段CD上取点F,使得DF=3CF,连接OP、OF、FQ
∵△ACD中,AQ=3QC且DF=3CF,∴QF∥AD且QF=
AD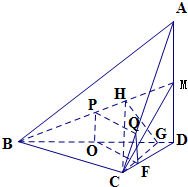
∵△BDM中,O、P分别为BD、BM的中点
∴OP∥DM,且OP=
DM,结合M为AD中点得:OP∥AD且OP=
AD
∴OP∥QF且OP=QF,可得四边形OPQF是平行四边形
∴PQ∥OF
∵PQ?平面BCD且OF?平面BCD,∴PQ∥平面BCD;
(Ⅱ)过点C作CG⊥BD,垂足为G,过G作GH⊥BM于H,连接CH
∵AD⊥平面BCD,CG?平面BCD,∴AD⊥CG
又∵CG⊥BD,AD、BD是平面ABD内的相交直线
∴CG⊥平面ABD,结合BM?平面ABD,得CG⊥BM
∵GH⊥BM,CG、GH是平面CGH内的相交直线
∴BM⊥平面CGH,可得BM⊥CH
因此,∠CHG是二面角C-BM-D的平面角,可得∠CHG=60°
设∠BDC=θ,可得
Rt△BCD中,CD=BDcosθ=2
cosθ,CG=CDsinθ=2
sinθcosθ,BG=BCsinθ=2
sin2θ
Rt△BMD中,HG=
=
sin2θ;Rt△CHG中,tan∠CHG=
=
=
∴tanθ=
,可得θ=60°,即∠BDC=60°,
∵BD=2
,
∴CD=
,
∴S△BCD=
×2
×
×
=
,
∴VA-BCD=
×
×2=
.
∵△ACD中,AQ=3QC且DF=3CF,∴QF∥AD且QF=
| 1 |
| 4 |

∵△BDM中,O、P分别为BD、BM的中点
∴OP∥DM,且OP=
| 1 |
| 2 |
| 1 |
| 4 |
∴OP∥QF且OP=QF,可得四边形OPQF是平行四边形
∴PQ∥OF
∵PQ?平面BCD且OF?平面BCD,∴PQ∥平面BCD;
(Ⅱ)过点C作CG⊥BD,垂足为G,过G作GH⊥BM于H,连接CH
∵AD⊥平面BCD,CG?平面BCD,∴AD⊥CG
又∵CG⊥BD,AD、BD是平面ABD内的相交直线
∴CG⊥平面ABD,结合BM?平面ABD,得CG⊥BM
∵GH⊥BM,CG、GH是平面CGH内的相交直线
∴BM⊥平面CGH,可得BM⊥CH
因此,∠CHG是二面角C-BM-D的平面角,可得∠CHG=60°
设∠BDC=θ,可得
Rt△BCD中,CD=BDcosθ=2
| 2 |
| 2 |
| 2 |
Rt△BMD中,HG=
| BG•DM |
| BM |
2
| ||
| 3 |
| CG |
| GH |
| 3cosθ |
| sinθ |
| 3 |
∴tanθ=
| 3 |
∵BD=2
| 2 |
∴CD=
| 2 |
∴S△BCD=
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
∴VA-BCD=
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
点评:本题在底面为直角三角形且过锐角顶点的侧棱与底面垂直的三棱锥中求证线面平行,并且在已知二面角大小的情况下求线线角.着重考查了线面平行、线面垂直的判定与性质,解直角三角形和平面与平面所成角求法等知识,属于中档题.

练习册系列答案
相关题目
 运行如图所示的程序框图,若输出的结果为
运行如图所示的程序框图,若输出的结果为| 13 |
| 7 |
| A、k≤5? | B、k≤6? |
| C、k≤7? | D、k≤8? |
正方形ABCD沿对角线AC折成直二面角,则异面直线AD和BC所成角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|