Question

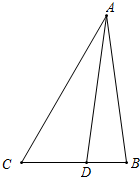如图，在△ABC中，已知4sin²

A-B

2

+4sinAsinB=3．
（I）求角C的大小；
（Ⅱ）若AC=8，点D在BC边上，且BD=2，cos∠ADB=

1

7

，求边AB的长．

Answer 1

考点：余弦定理,两角和与差的正弦函数

专题：解三角形

分析：（I）已知等式利用二倍角的余弦函数公式化简，再利用两角和与差的余弦函数公式化简，求出cosC的值，即可确定出角C的大小；
（Ⅱ）由cos∠ADB的值求出cos∠ADC的值，进而求出sin∠ADC的值，再由sinC与AC的长，利用正弦定理求出AD的长，再利用余弦定理求出AB的长即可．

解答： 解：（I）由4sin²

A-B

2

+4sinAsinB=3，
变形得：2[1-cos（A-B）]+4sinAsinB=3，
即2-2（cosAcosB+sinAsinB）+4sinAsinB=3，
整理得：2-2cos（A+B）=3，即2+2cosC=3，
∴cosC=

1

2

，
则C=

π

3

；

（Ⅱ）∵cos∠ADB=

1

7

，∠ADB+∠ADC=π，
∴cos∠ADC=-

1

7

，sin∠ADC=

4 3

7

，
在△ADC中，由正弦定理

AD

sinC

=

AC

sin∠ADC

得：AD=

ACsinC

sin∠ADC

=

8× 3 2

4 3 7

=7，
由余弦定理得：AB²=DA²+DB²-2DA•DB•cos∠ADB=49+4-4=49，
则AB=7．

点评：此题考查了正弦、余弦定理，以及同角三角函数间的基本关系，熟练掌握定理是解本题的关键．