题目内容
在区间[0,1]上任取2个数a,b,若向量
=(a,b),则|
|≤1的概率是( )
| m |
| m |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:先求出满足向量|
|≤1的轨迹,然后利用几何概型的公式去求概率.
| m |
解答:
解:设
,则M(a,b).由题意知a,b∈[0,1],
故点M对应的基本事件Ω是一个边长为1的正方形,所以它的面积为1.
记向量|
|≤1对应的事件为P,因为向量|
|≤1,得aa2+b2≤1,
即事件P对应的基本事件空间是以坐标原点为圆心,半径为1的圆在第一象限内的部分,其面积为
π,
即|
|≤1的概率是
=
.
故选D
| OM |
故点M对应的基本事件Ω是一个边长为1的正方形,所以它的面积为1.
记向量|
| m |
| m |
即事件P对应的基本事件空间是以坐标原点为圆心,半径为1的圆在第一象限内的部分,其面积为
| 1 |
| 4 |
即|
| m |
| ||
| 1 |
| π |
| 4 |
故选D
点评:本题的考点是与面积有关几何概型,首先利用条件将事件转化为对应的平面图形是解决本题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
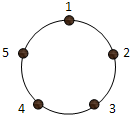 如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按瞬时针方向绕圆从一个点跳到下一个点.若它停在奇数点上,则下一次只能跳一个点,若停在偶数点上,则可以连续跳2个点.该青蛙从5这点起跳,经2009次跳后它将停在的点是( )
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按瞬时针方向绕圆从一个点跳到下一个点.若它停在奇数点上,则下一次只能跳一个点,若停在偶数点上,则可以连续跳2个点.该青蛙从5这点起跳,经2009次跳后它将停在的点是( )| A、1 | B、2 | C、3 | D、4 |
已知
=(-2,0),
=(0,2)(O为坐标原点),点C在曲线
(θ为参数)上运动,则△ABC面积的最大值为( )
| OA |
| OB |
|
A、3-
| ||||
B、3+
| ||||
C、
| ||||
D、
|
设2x=5y=m,且
+
=2,则m的值是( )
| 1 |
| x |
| 1 |
| y |
A、±
| ||
B、
| ||
| C、10 | ||
| D、100 |
已知点P(x,y)的坐标满足条件:
,则
x+y的最小值为( )
|
| 3 |
A、
| ||
| B、0 | ||
C、-
| ||
D、-
|
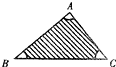 △ABC中,AB=8,AC=6,BC=10,顶点A、B、C处分别有一枚半径为1的硬币(顶点A、B、C分别与硬币的中心重合).向△ABC内部投一点,那么该点落在阴影部分的概率为( )
△ABC中,AB=8,AC=6,BC=10,顶点A、B、C处分别有一枚半径为1的硬币(顶点A、B、C分别与硬币的中心重合).向△ABC内部投一点,那么该点落在阴影部分的概率为( )A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
已知平面向量
=(2,1),
=(-4,k),且
⊥
,则3
+2
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(-2,4) |
| B、( 4,7) |
| C、(-2,19) |
| D、(19,2) |
当x∈[0,π]时,函数f(x)=cosx-
sinx的值域是( )
| 3 |
| A、[-2,1] | ||
| B、[-1,2] | ||
| C、[-1,1] | ||
D、[-2,
|
 已知函数
已知函数