题目内容
数列{an}满足an+1=
,若a1=
,则a2015=( )
|
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:根据数列的递推关系得到数列为周期数列即可得到结论
解答:
解:由递推数列可得,
a1=
,a2=2a1-1=2×
-1=
,
a3=2a2-1=2×
-1=
,
a4=2a3=2×
=
,
a5=2a4=2×
=
,
…
∴a5=a1,
即an+4=an,
则数列{an}是周期为4的周期数列,
则a2015=a503×4+3=a3=
,
故选:A
a1=
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
a3=2a2-1=2×
| 3 |
| 5 |
| 1 |
| 5 |
a4=2a3=2×
| 1 |
| 5 |
| 2 |
| 5 |
a5=2a4=2×
| 2 |
| 5 |
| 4 |
| 5 |
…
∴a5=a1,
即an+4=an,
则数列{an}是周期为4的周期数列,
则a2015=a503×4+3=a3=
| 1 |
| 5 |
故选:A
点评:本题主要考查递推数列的应用,根据递推关系得到数列{an}是周期为4的周期数列是解决本题的关键

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
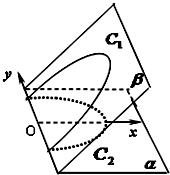 如右图二面角α-y-β的大小为60°,平面β上的曲线C1在平面α上的正射影为曲线C2,C2在直角坐标系xOy下的方程x2+y2=1(0≤x≤1),则曲线C1的离心率( )
如右图二面角α-y-β的大小为60°,平面β上的曲线C1在平面α上的正射影为曲线C2,C2在直角坐标系xOy下的方程x2+y2=1(0≤x≤1),则曲线C1的离心率( )| A、e=1 | ||||
| B、e>1 | ||||
C、e=
| ||||
D、e=
|
