题目内容
设a∈R,f(x)=
(x∈R)是奇函数,
(1)求a的值;
(2)解不等式f(1-5x)+f(6x2)>0.
| a•2x+a-2 |
| 2x+1 |
(1)求a的值;
(2)解不等式f(1-5x)+f(6x2)>0.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据函数的定义域是R且是奇函数,得f(0)=0可求得实数a的值;
(2)将解析式分离常数后判断出单调性,再利用定义法证明函数的单调性,利用函数的奇偶性将不等式转化为:f(1-5x)>-f(6x2)=f(-6x2),然后利用单调性解不等式.
(2)将解析式分离常数后判断出单调性,再利用定义法证明函数的单调性,利用函数的奇偶性将不等式转化为:f(1-5x)>-f(6x2)=f(-6x2),然后利用单调性解不等式.
解答:
解:(1)∵f(x)=
的定义域为R,且是奇函数,
∴f(0)=
=0,解得a=1,
(2)由(1)得,f(x)=
=1-
,
∴f(x)=1-
在R上单调递增函数,
证明如下:设x1<x2,
f(x1)-f(x2)=1-
-(1-
)
=
<0,
∴f(x1)<f(x2),
即f(x)在(-∞,+∞)上为增函数,
由f(1-5x)+f(6x2)>0得,f(1-5x)>-f(6x2)=f(-6x2),
∴1-5x>-6x2,即6x2-5x+1>0,
解得x>
或x<
,
故不等式的解集为:{x|x>
或x<
}.
| a•2x+a-2 |
| 2x+1 |
∴f(0)=
| a+a-2 |
| 2+1 |
(2)由(1)得,f(x)=
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
∴f(x)=1-
| 2 |
| 2x+1 |
证明如下:设x1<x2,
f(x1)-f(x2)=1-
| 2 |
| 2x1+1 |
| 2 |
| 2x2+1 |
=
| 2(2x1-2x2) |
| (2x1+1)(2x2+1) |
∴f(x1)<f(x2),
即f(x)在(-∞,+∞)上为增函数,
由f(1-5x)+f(6x2)>0得,f(1-5x)>-f(6x2)=f(-6x2),
∴1-5x>-6x2,即6x2-5x+1>0,
解得x>
| 1 |
| 2 |
| 1 |
| 3 |
故不等式的解集为:{x|x>
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题主要考查函数奇偶性的应用,利用定义法证明函数的单调性,以及函数单调性和奇偶性的综合应用,利用函数的奇偶性将不等式进行转化是解决本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
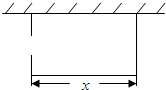 某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.