题目内容
在平面直角坐标系xOy中,不等式组
表示的平面区域为W,从区域W中随机点M(x,y).
(1)若x∈R,y∈R,求OM≥1得概率;
(2)若x∈Z,y∈Z,求点M位于第二象限的概率.
|
(1)若x∈R,y∈R,求OM≥1得概率;
(2)若x∈Z,y∈Z,求点M位于第二象限的概率.
考点:几何概型
专题:计算题,概率与统计
分析:(1)这是一个几何概率模型.算出图中以(0,0)圆心1为半径的圆的面积,再除以平面区域矩形面积,即可求出概率.
(2)确定平面区域整数点坐标个数,再找出第二象限中的点个数.二者做除法即可算出概率.
(2)确定平面区域整数点坐标个数,再找出第二象限中的点个数.二者做除法即可算出概率.
解答:
解:(1)这是一个几何概率模型.OM=1时,半圆的面积为
π,
若x,y∈R,则区域W的面积是3×2=6.
∴满足OM≥1的点M构成的区域的面积为6-
π,
∴OM≥1的概率为
=1-
;
(2)若x,y∈Z,则点M的个数共有12个,列举如下:
(-1,0),(-1,1),(-1,2),(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2).
当点M的坐标为(-1,1),(-1,2)时,点M位于第二象限,
故点M位于第二象限的概率为
=
.
| 1 |
| 2 |
若x,y∈R,则区域W的面积是3×2=6.
∴满足OM≥1的点M构成的区域的面积为6-
| 1 |
| 2 |
∴OM≥1的概率为
6-
| ||
| 6 |
| π |
| 12 |
(2)若x,y∈Z,则点M的个数共有12个,列举如下:
(-1,0),(-1,1),(-1,2),(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2).
当点M的坐标为(-1,1),(-1,2)时,点M位于第二象限,
故点M位于第二象限的概率为
| 2 |
| 12 |
| 1 |
| 6 |
点评:概率模型包括古典概型与几何概型,区分的方法在于基本事件的有限与无限.

练习册系列答案
相关题目
α为平面,m,n是两条不同直线,则m∥n的一个充分条件是( )
| A、m∥α且n∥α |
| B、m,n与平面α所成的角相等 |
| C、m⊥α且n⊥α |
| D、m,n与平面α的距离相等 |
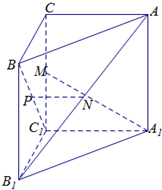 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=