Question

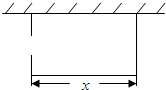某校要建一个面积为450平方米的矩形球场，要求球场的一面利用旧墙，其他各面用钢筋网围成，且在矩形一边的钢筋网的正中间要留一个3米的进出口（如图）．设矩形的长为x米，钢筋网的总长度为y米．
（Ⅰ）列出y与x的函数关系式，并写出其定义域；
（Ⅱ）问矩形的长与宽各为多少米时，所用的钢筋网的总长度最小？
（Ⅲ）若由于地形限制，该球场的长和宽都不能超过25米，问矩形的长与宽各为多少米时，所用的钢筋网的总长度最小？

Answer 1

考点：函数解析式的求解及常用方法,函数的最值及其几何意义,基本不等式

专题：综合题

分析：第一问较简单，别忘记写定义域；第二问用到基本不等式的性质注意能否取到“=”；第三问在求函数的单调区间时可以用导数求，也可以用函数单调性的定义求解，都能得到y在（0，25]上是单调递减函数；再求出函数最值．

解答： 解：（Ⅰ）∵矩形的宽为：

450

x

米，
∴y=2•

450

x

-3+x=

900

x

+x-3 定义域为{x|0＜x＜150}；
（Ⅱ）y=

900

x

+x-3≥2

900 x •x

-3=60-3=57
当且仅当

900 x =x x＞0

即x=30时取等号，此时宽为：

450

x

=15米，
∴长为30米，宽为15米，所用的钢筋网的总长度最小．     
（Ⅲ）法一：y=

900

x

+x-3（0＜x≤25），∵y′=-

900

x2

+1=

(x+30)(x-30)

x2

∴当0＜x≤25时，x+30＞0，x-30＜0，x²＞0∴y'＜0∴y在（0，25]上是单调递减函数  
∴当x=25时，ymin=

900

25

+25-3=58，此时，长为25米，宽为

450

x

=18米
所以，长为25米，宽为18米时，所用的钢筋网的总长度最小．  
法二：设f(x)=

900

x

+x-3(0＜x≤25)，0＜x₁＜x₂≤25，
则 f(x2)-f(x1)=(

900

x2

+x2)-(

900

x1

+x1)=

(x2-x1)(x1x2-900)

x1x2

；
∵0＜x₁＜x₂≤25，∴x₂-x₁＞0，x₁x₂＞0，x₁x₂-900＜0∴f（x₂）-f（x₁）＜0，
∴f（x₂）＜f（x₁）∴f（x）在（0，25]上是单调递减函数；
∴当x=25时，fmin(x)=f(25)=

900

25

+25-3=58
此时，长为25米，宽为

450

x

=18米
所以，长为25米，宽为18米时，所用的钢筋网的总长度最小．

点评：本题主要考查基本不等式的应用，考查了函数的单调性，最值；考查运算求解的能力，考查应用意识、函数与方程、化归与转化等数学思想．