题目内容
5.已知函数f(x)=ax2+(b-1)x+1(a,b∈R,a>0).(1)若f(1)=0,且对任意x∈R,都有f(2-x)=f(2+x),求f(x)的解析式;
(2)已知x1,x2为函数f(x)的两个零点,且x2-x1=2,当x∈(x1,x2)时,g(x)=-f(x)+2(x2-x)的最大值为h(a),当a≥2时,求h(a)的最小值.
分析 (1)由f(2-x)=f(2+x)得函数的对称轴为x=2,结合一元二次函数的对称性进行求解即可,求f(x);
(2)求出g(x)=a(x2-x)(x-x1+$\frac{2}{a}$),根据基本不等式求出g(x)≤a+$\frac{1}{a}$+2,利用函数的单调性求出答案.
解答 解:(1)由f(2-x)=f(2+x),得函数f(x)关于x=2对称,则-$\frac{b-1}{2a}$=2,
又a+b-1+1=0,
解得a=$\frac{1}{3}$,b=-$\frac{1}{3}$,
∴f(x)=$\frac{1}{3}$x2-$\frac{4}{3}$x+1;
(2)设f(x)=a(x-x1)(x-x2),
g(x)=-a(x-x1)(x-x2)+2(x2-x)=-a(x-x2)(x-x1+$\frac{2}{a}$)=a(x2-x)(x-x1+$\frac{2}{a}$);
∵x∈(x1,x2),a≥2;
∴x2-x>0,x-x1+$\frac{2}{a}$>0;
∵$\frac{{x}_{1}+{x}_{2}}{2}$-$\frac{1}{a}$-x2═$\frac{{x}_{1}-{x}_{2}}{2}$-$\frac{1}{a}$=$\frac{-2}{2}$-$\frac{1}{a}$=1-$\frac{1}{a}$<0,
∴$\frac{{x}_{1}+{x}_{2}}{2}$-$\frac{1}{a}$<x2,
$\frac{{x}_{1}+{x}_{2}}{2}$-$\frac{1}{a}$-x2=$\frac{{x}_{1}-{x}_{2}}{2}$-$\frac{1}{a}$=1-$\frac{1}{a}$>1-$\frac{1}{2}$=$\frac{1}{2}$>0,
∴$\frac{{x}_{1}+{x}_{2}}{2}$-$\frac{1}{a}$>x1,
∴x=$\frac{{x}_{1}+{x}_{2}}{2}$-$\frac{1}{a}$∈(x1,x2).
∴g(x)≤a•($\frac{{x}_{2}-{x}_{1}+\frac{2}{a}}{2}$)2=a+$\frac{1}{a}$+2,
当x=$\frac{{x}_{1}+{x}_{2}}{2}$-$\frac{1}{a}$=$\frac{-b-1}{2a}$时取“=”;
∴h(a)=a+$\frac{1}{a}$+2,a≥2;
a≥2时,h′(x)=1-$\frac{1}{{a}^{2}}$>0;
∴h(a)在[2,+∞)上单调递增;
∴h(2)=$\frac{9}{2}$是h(a)的最小值.
点评 本题主要考查一元二次函数的性质,考查学生的运算能力,综合性较强,难度较大.

| A. | $\left\{\begin{array}{l}x={t^{\frac{1}{2}}}\\ y={t^{-\frac{1}{2}}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}x={2^t}\\ y={2^{-t}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=log_2t\\ y=log_t2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=sinα\\ y=\frac{1}{sinα}\end{array}\right.$ |
| A. | $\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=2\sqrt{t}}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=2t+1}\\{y=4t+1}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=cosθ}\\{y=2sinθ}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=tanθ}\\{y=2tanθ}\end{array}}\right.$ |

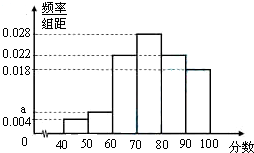 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]