题目内容
已知a＞0，x、y满足约束条件
，若z=2x+y的最小值为0，则a=（ ）
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式对应的平面区域，利用线性规划的知识，通过平移即先确定z的最优解，然后确定a的值即可．
解答：
解：作出不等式对应的平面区域，（阴影部分）
由z=2x+y，得y=-2x+z，
平移直线y=-2x+z，由图象可知当直线y=-2x+z经过点B时，直线y=-2x+z的截距最小，此时z最小为0，即2x+y=0．
由
，解
，
即B（1，-2），
∵点B也在直线y=a（x-3）上，即-2=-2a，
解得a=1．
故选：C．
由z=2x+y，得y=-2x+z，
平移直线y=-2x+z，由图象可知当直线y=-2x+z经过点B时，直线y=-2x+z的截距最小，此时z最小为0，即2x+y=0．
由
|
|
即B（1，-2），
∵点B也在直线y=a（x-3）上，即-2=-2a，
解得a=1．
故选：C．
点评：本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．
练习册系列答案
相关题目
某奶茶店为了了解奶茶销售量与气温之间的关系，随机统计并制作了6天卖出的奶茶的杯数与气温的对照表：
经检验，这组样本数据具有线性相关关系，那么，对于气温x（℃）与奶茶销售量y这两个变量，下列判断正确的是（ ）
| 气温x（℃） | 26 | 19 | 14 | 10 | 4 | -1 |
| 杯数y | 201 | 242 | 339 | 383 | 505 | 640 |
| A、成正相关，其回归直线经过点（13，385） |
| B、成负相关，其回归直线经过点（13，386） |
| C、成正相关，其回归直线经过点（12，386） |
| D、成负相关，其回归直线经过点（12，385） |
下列命题正确的是（ ）
| A、如果a，b是两条直线，且a∥b，那么a平行于经过b的任何平面 |
| B、如果直线a和平面α满足a∥α，那么a与α内的任何直线平行 |
| C、如果直线a，b和平面α满足a∥α，b∥α，那么a∥b |
| D、如果直线a，b和平面α满足a∥b，a∥α，b?α，那么b∥α |
已知双曲线
-
=1(b＞a＞0)的两条渐近线为l1，l2，过右焦点F作垂直l1的直线交l1，l2于A，B两点．若|OA|，|AB|，|OB|成等差数列，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
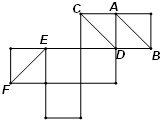如图是一个正方体纸展开图，如果将它还原成正方体，那么直线AB，CD，EF在原正方体的位置关系是（ ）| A、AB∥CD，EF⊥CD |
| B、AB与CD异面成角60°，CD与EF相交成角60° |
| C、AB∥CD，CD与EF相交成角60° |
| D、EF⊥CD，AB与CD异面成角60° |
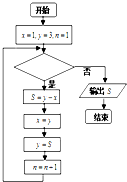已知数列{an}满足a1=1，a2=3，an+2=an+1-an，n∈N*，利用如图所示的程序框图计算该数列的第n项（n≥3），若输出S的结果为1，则判断框内的条件可能是（ ）| A、n≤5？ | B、n≤6？ |
| C、n≤7？ | D、n≤8？ |
函数f（x）=x2-ax+2在（2，+∞）上单调递增，则a的取值范围为（ ）
| A、[2，+∞） |
| B、[4，+∞） |
| C、（-∞，4] |
| D、（-∞，-4] |
“x=2”是“log2|x|=1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |