��Ŀ����
����������{an}��n��N*���У�SnΪ{an}��ǰn��ͣ����㣨an��Sn���ں���y=
��ͼ���ϣ�����cΪ����������c��1��
����������{an}��ͨ�ʽ��
�����Ƿ����������M��ʹ�õ�n��Mʱ��a1•a3•a5��a2n-1��a101������������ڣ����ʹ���۳�����c��ȡֵ��Χ����Ӧ��M����Сֵ��
����������һ���Ȳ�����{bn}��������n��N*������b1an+b2an-1+b3an-2+��+bn-1a2+bna1=3n-
n-1��������{bn}��ͨ�ʽ��c��ֵ��
| c2-x |
| c-1 |
����������{an}��ͨ�ʽ��
�����Ƿ����������M��ʹ�õ�n��Mʱ��a1•a3•a5��a2n-1��a101������������ڣ����ʹ���۳�����c��ȡֵ��Χ����Ӧ��M����Сֵ��
����������һ���Ȳ�����{bn}��������n��N*������b1an+b2an-1+b3an-2+��+bn-1a2+bna1=3n-
| 5 |
| 3 |
���㣺�����벻��ʽ���ۺ�,���еĺ�������
ר�⣺������,�Ȳ�������ȱ�����
�����������ɵ㣨an��Sn���ں���ͼ���ϣ����뺯������ʽ�ɵõ�an��Sn�Ĺ�ϵʽ����sn����an��
�������˺����������ת����ָ�����㷨��ͬʱҲ�����˷������۵�˼�룮
�������˴�λ������ı���Ӧ�ü����������ij�����������
�������˺����������ת����ָ�����㷨��ͬʱҲ�����˷������۵�˼�룮
�������˴�λ������ı���Ӧ�ü����������ij�����������
���
�⣺����sn=
��n��2ʱ��sn-sn-1=
-
an=
��(c-1)an=an-1-an��can=an-1��
=
��{an}�ǵȱ����У�
����a1��S1������y=
��a1=c��
��an=(
)n-2��
������a1•a3•a5��a2n-1��a101����c•c-1��(
)2n-3��(
)99��
��(
)n(n-2)��(
)99��
��
��1����0��c��1ʱ��n(n-2)��99��
��ã�n��11��n��-9����ȥ����
��
��1����c��1ʱ��n(n-2)��99��
��ã�-9��n��11��
������n��Mʱ��a1•a3•a5��a2n-1��a101�����������ȥ��
c��ȡֵ��Χ�ǣ�0��1������Ӧ��M����СֵΪ11��
�����ɣ���֪��an=c2-n����{bn}Ϊ�Ȳ����У���bn=b1+��n-1��d��
b1an+b2an-1+��+bn-1a2+bna1=3n-
n-1��n��N*������1��
��n=1ʱ��b1c=
����2��
��n��2ʱ��b1an-1+b2an-2+��+bn-2a2+bn-1a1=3n-1-
(n-1)-2����3��
��1��-��3����b1an+d��an-1+an-2+��+a1��=3n-3n-1-
��
����b1c-
��c1-n+
=2��3n-1-
����4��
�ߣ�4��ʽ��һ��n��n��2��������������
�⣨2����5����
��bbn=10n-9��c=
��
| c2-an |
| c-1 |
| c2-an |
| c-1 |
| c2-an-1 |
| c-1 |
an=
| an-1-an |
| c-1 |
| an |
| an-1 |
| 1 |
| c |
��{an}�ǵȱ����У�
����a1��S1������y=
| c2-x |
| c-1 |
��an=(
| 1 |
| c |
������a1•a3•a5��a2n-1��a101����c•c-1��(
| 1 |
| c |
| 1 |
| c |
��(
| 1 |
| c |
| 1 |
| c |
��
| 1 |
| c |
��ã�n��11��n��-9����ȥ����
��
| 1 |
| c |
��ã�-9��n��11��
������n��Mʱ��a1•a3•a5��a2n-1��a101�����������ȥ��
c��ȡֵ��Χ�ǣ�0��1������Ӧ��M����СֵΪ11��
�����ɣ���֪��an=c2-n����{bn}Ϊ�Ȳ����У���bn=b1+��n-1��d��
b1an+b2an-1+��+bn-1a2+bna1=3n-
| 5 |
| 3 |
��n=1ʱ��b1c=
| 1 |
| 3 |
��n��2ʱ��b1an-1+b2an-2+��+bn-2a2+bn-1a1=3n-1-
| 5 |
| 3 |
��1��-��3����b1an+d��an-1+an-2+��+a1��=3n-3n-1-
| 5 |
| 3 |
����b1c-
| c2d |
| c-1 |
| c2d |
| c-1 |
| 5 |
| 3 |
�ߣ�4��ʽ��һ��n��n��2��������������
|
�⣨2����5����
|
| 1 |
| 3 |
����������������Ϊ���壬�������������е���ͷ�������ͨ�ʽ�ķ��������ҿ����˺��������Ĵ����������ۺ��ԱȽ�ǿ������ܷ�����ѧ����ͨ������ϰ���գ�

��ϰ��ϵ�д�
�����Ŀ
ִ����ͼ��ʾ�ij����ͼ������Ľ����15����a�ij�ʼֵm��m��0���ж����ֿ��ܣ�������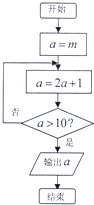

| A��1 | B��2 | C��3 | D��4 |


