题目内容
已知函数f(x)=
x3-
(a+2)x2+2ax-a2(a∈R).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图象与直线y=m有三个交点,求m的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图象与直线y=m有三个交点,求m的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由已知条件推导出函数定义域为x∈R,f′(x)=x2-(a+2)x+2a=(x-a)(x-2),由此根据a的取值范围进行分类讨论,能求出f(x)的单调区间.
(Ⅱ)若a=4,由(Ⅰ)可得f(x)在(-∞,2]上单调递增,在[4,+∞)上单调递增,在[2,4]上单调递减.由此能求出f(x)的极值,从而能求出y=f(x)的图象与直线y=m有三个交点时m的取值范围.
(Ⅱ)若a=4,由(Ⅰ)可得f(x)在(-∞,2]上单调递增,在[4,+∞)上单调递增,在[2,4]上单调递减.由此能求出f(x)的极值,从而能求出y=f(x)的图象与直线y=m有三个交点时m的取值范围.
解答:
解:(Ⅰ)函数f(x)=
x3-
(a+2)x2+2ax-a2的定义域为x∈R,
f′(x)=x2-(a+2)x+2a=(x-a)(x-2),(2分)
①当a=2时,f'(x)≥0恒成立,f(x)在R上是增函数.(4分)
②当a<2时,f'(x)≥0在(-∞,a]和[2,+∞)上恒成立,
f′(x)≤0在[a,2]上恒成立.
∴a<2时f(x)的增区间为(-∞,a],[2,+∞),f(x)的减区间为[a,2].(6分)
③当a>2时,f′(x)≥0在(-∞,2]和[a,+∞)上恒成立,
f′(x)≤0在[2,a]上恒成立,
∴a>2时,f(x)的增区间为(-∞,2]和[a,+∞),f(x)的减区间为[2,a].(8分)
(Ⅱ)若a=4,由(Ⅰ)可得f(x)在(-∞,2]上单调递增,
在[4,+∞)上单调递增,在[2,4]上单调递减.(10分)
∴f(x)极小值=f(4)=-
,(11分)f(x)极大值=f(2)=-
,(12分)
∴y=f(x)的图象与直线y=m有三个交点时m的取值范围是(-
,-
).(14分)
| 1 |
| 3 |
| 1 |
| 2 |
f′(x)=x2-(a+2)x+2a=(x-a)(x-2),(2分)
①当a=2时,f'(x)≥0恒成立,f(x)在R上是增函数.(4分)
②当a<2时,f'(x)≥0在(-∞,a]和[2,+∞)上恒成立,
f′(x)≤0在[a,2]上恒成立.
∴a<2时f(x)的增区间为(-∞,a],[2,+∞),f(x)的减区间为[a,2].(6分)
③当a>2时,f′(x)≥0在(-∞,2]和[a,+∞)上恒成立,
f′(x)≤0在[2,a]上恒成立,
∴a>2时,f(x)的增区间为(-∞,2]和[a,+∞),f(x)的减区间为[2,a].(8分)
(Ⅱ)若a=4,由(Ⅰ)可得f(x)在(-∞,2]上单调递增,
在[4,+∞)上单调递增,在[2,4]上单调递减.(10分)
∴f(x)极小值=f(4)=-
| 32 |
| 3 |
| 28 |
| 3 |
∴y=f(x)的图象与直线y=m有三个交点时m的取值范围是(-
| 32 |
| 3 |
| 28 |
| 3 |
点评:本题考查函数的单调区间的求法,考查实数的取值范围的求法,解题时要认真审题,注意导数性质的灵活运用和分类讨论思想的合理运用.

练习册系列答案
相关题目
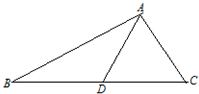 如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且
如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且