题目内容
在研究PM2.5(霾的主要成分)形成原因时,某研究人员研究了PM2.5与燃烧排放的CO2,NO2,CO,O3等物质的相关关系,如图是PM2.5与CO,O3相关性的散点图,
(Ⅰ)根据三点图,请你就CO,O3对PM2.5的影响关系作出初步评价;
(Ⅱ)以100μg/m3为单位,在上述左图中取三个点,如下表所示,
求
关于
的回归方程,并估计当CO的排放量为200μg/m3时,PM2.5的值(用最小二乘法求回归方程的系数是(b=
,a=
-b
)
(Ⅲ)雾霾对交通影响较大,某市交通部门发现,在一个月内,当CO排放量(单位:μg/m3)分别是60,120,180时,某路口的交通流量(单位:万辆)依次是800,600,200,在一个月内,CO排放量是60,120,180的概率依次是p,q,r,且ρ≤
,3ρ≤4r,求该路口一个月的交通流量期望值的最大值.

(Ⅰ)根据三点图,请你就CO,O3对PM2.5的影响关系作出初步评价;
(Ⅱ)以100μg/m3为单位,在上述左图中取三个点,如下表所示,
| PM2.5(x) | 1 | 2 | 4 |
| CO(y) | 0.5 | 1 | 1.5 |
 |
| y |
 |
| x |
| |||||||
|
. |
| y |
. |
| x |
(Ⅲ)雾霾对交通影响较大,某市交通部门发现,在一个月内,当CO排放量(单位:μg/m3)分别是60,120,180时,某路口的交通流量(单位:万辆)依次是800,600,200,在一个月内,CO排放量是60,120,180的概率依次是p,q,r,且ρ≤
| 1 |
| 3 |
考点:线性回归方程
专题:概率与统计
分析:(I)根据左图的散点分布在一个条形区域内,可得CO与PM2.5具有正相关关系,而右图散点之间分布较散不具有较强的相关关系;
(II)根据已知表中数据计算出
,
,
,
yi,求出回归直线方程,再将点的坐标代入回归直线方程可估计当CO的排放量为200μg/m3时,PM2.5的值;
(III)p,q,r满足约束条件
,目标函数E(X)=200(3p+2q)+200,进而可得交通流量期望值的最大值.
(II)根据已知表中数据计算出
. |
| x |
. |
| y |
| 3 |
 |
| i=1 |
| x | 2 i |
| 3 |
 |
| i=1 |
| x | i |
(III)p,q,r满足约束条件
|
解答:
解:(I)由已知中的散点图,可得CO与PM2.5具有正相关关系,O3与PM2.5不存在相关关系;
(II)∵
=
,
=1,
=21,
yi=8.5,
∴b=
=
=
,
a=
-b
=
,
∴
关于
的回归方程为
=
x+
,
当CO的排放量为200μg/m3时,PM2.5的值
x+
=2,
解得:
=
,即PM2.5的值为
×100≈544μg/m3;
(III)设交通流量是X,则X可以取800,600,200,
则X的分布列如下表所示:
∵
,
∴
,
交通流量X的期望值E(X)=800p+600q+200r=200(3p+2q)+200,
当p=
且q=
时,交通流量X的期望值E(X)取最大值200(3×
+2×
)+200≈552.38万辆,
即交通流量最大为552.38万辆.
(II)∵
. |
| x |
| 7 |
| 3 |
. |
| y |
| 3 |
 |
| i=1 |
| x | 2 i |
| 3 |
 |
| i=1 |
| x | i |
∴b=
| |||||||||
|
8.5-3×
| ||
21-3×(
|
| 9 |
| 28 |
a=
. |
| y |
. |
| x |
| 1 |
| 4 |
∴
 |
| y |
 |
| x |
 |
| y |
| 9 |
| 28 |
| 1 |
| 4 |
当CO的排放量为200μg/m3时,PM2.5的值
| 9 |
| 28 |
| 1 |
| 4 |
解得:
 |
| x |
| 49 |
| 9 |
| 49 |
| 9 |
(III)设交通流量是X,则X可以取800,600,200,
则X的分布列如下表所示:
| X | 800 | 600 | 200 |
| P | p | q | r |
|
∴
|
交通流量X的期望值E(X)=800p+600q+200r=200(3p+2q)+200,
当p=
| 1 |
| 3 |
| 8 |
| 21 |
| 1 |
| 3 |
| 8 |
| 21 |
即交通流量最大为552.38万辆.
点评:统计也是高考新增的考点,回归直线方程的求法,又是统计中的一个重要知识点,其系数公式及性质要求大家要熟练掌握并应用.

练习册系列答案
相关题目
已知a2+b2≤1,则关于x的方程x2-2ax+b2=0有两个不同的实数根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
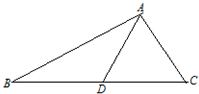 如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且
如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且