题目内容
数列{an}中,a1=1,a2=2,且an+2-an=1+(-1)n(n∈N+).
(1)求数列{an}的通项公式.
(2)求数列{an}的前n项和Sn.
(3)若Sn>t•n-4对于n∈N*恒成立,求t的取值范围.
(1)求数列{an}的通项公式.
(2)求数列{an}的前n项和Sn.
(3)若Sn>t•n-4对于n∈N*恒成立,求t的取值范围.
考点:数列递推式
专题:等差数列与等比数列
分析:(1)分情况讨论,n为奇数和偶数时,an的取值即可.
(2)分情况讨论,n为奇数和偶数时分别求和,求和是利用分组求和法.
(3)恒成立问题要先分离变量,后利用基本不等式解决.
(2)分情况讨论,n为奇数和偶数时分别求和,求和是利用分组求和法.
(3)恒成立问题要先分离变量,后利用基本不等式解决.
解答:
解:(1)∵an+2-an=1+(-1)n(n∈N+)
当n为奇数时,an+2-an=0(n∈N*),
即an+2=an
∵a1=1,
∴当n为奇数时,an=1;
当n为偶数时,an+2-an=2(n∈N+),
即an+2=an+2(n∈N+),
∵a2=2,
∴a2k=2+(k-1)2=2k
∴当n为偶数时,an=n
∴an的通项公式为an=
(2)由(1)可知,
当n为偶数时,Sn=1+2+1+4+…+1+n=
+
=
当n为奇数时,Sn=Sn-1+1=
+1=
故Sn=
(3)∵Sn>t•n-4对于n∈N*恒成立,
∴由(2)可知
①当n为偶数时,即
>t•n-4恒成立
不等式转化为t<
∵
=
+
+1≥2+1=3,
当且仅当n=4时取等号
∴t<3
②当n为奇数时,即
>t•n-4恒成立
不等式转化为t<
,
∵
=
+
+
≥
+
当且仅当n=
时取等号,
∵n∈N*,
∴当n=3时
=
,
当n=5时
=
取最小值为
∴t<
综上所述,t的取值范围是t<
.
当n为奇数时,an+2-an=0(n∈N*),
即an+2=an
∵a1=1,
∴当n为奇数时,an=1;
当n为偶数时,an+2-an=2(n∈N+),
即an+2=an+2(n∈N+),
∵a2=2,
∴a2k=2+(k-1)2=2k
∴当n为偶数时,an=n
∴an的通项公式为an=
|
(2)由(1)可知,
当n为偶数时,Sn=1+2+1+4+…+1+n=
| n |
| 2 |
| ||
| 2 |
| n2+4n |
| 4 |
当n为奇数时,Sn=Sn-1+1=
| (n-1)2+4(n-1) |
| 4 |
| (n+1)2 |
| 4 |
故Sn=
|
(3)∵Sn>t•n-4对于n∈N*恒成立,
∴由(2)可知
①当n为偶数时,即
| n2+4n |
| 4 |
不等式转化为t<
| n2+4n+16 |
| 4n |
∵
| n2+4n+16 |
| 4n |
| n |
| 4 |
| 4 |
| n |
当且仅当n=4时取等号
∴t<3
②当n为奇数时,即
| (n+1)2 |
| 4 |
不等式转化为t<
| n2+2n+17 |
| 4n |
∵
| n2+2n+17 |
| 4n |
| n |
| 4 |
| 17 |
| 4n |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
当且仅当n=
| 17 |
∵n∈N*,
∴当n=3时
| n2+2n+17 |
| 4n |
| 8 |
| 3 |
当n=5时
| n2+2n+17 |
| 4n |
| 13 |
| 5 |
| 13 |
| 5 |
∴t<
| 13 |
| 5 |
综上所述,t的取值范围是t<
| 13 |
| 5 |
点评:本题考查了等比数列的定义,通项公式及前n项和公式,以及分类讨论的思想,综合运用了逐差求和法和分组求和法,难度较大.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
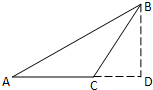 已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若
已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若| AB |
| a |
| AC |
| b |
| BD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设a,b,c∈R,且a<b,则( )
| A、ac>bc | ||||
B、
| ||||
| C、a2>b2 | ||||
| D、a3<b3 |
已知奇函数f(x)在区间[-2,2]上单调递减,则不等式f(x2)+f(2x)>0的解集是( )
| A、[-1,0) |
| B、(-2,0) |
| C、(-2,-1] |
| D、(-∞,-2)∪(0,+∞) |
已知直线l的斜率为k(k≠0),它在x轴、y轴上的截距分别为k、2k,则直线l的方程为( )
| A、2x-y-4=0 |
| B、2x-y+4=0 |
| C、2x+y-4=0 |
| D、2x+y+4=0 |