题目内容
已知直线l的斜率为k（k≠0），它在x轴、y轴上的截距分别为k、2k，则直线l的方程为（ ）
| A、2x-y-4=0 |
| B、2x-y+4=0 |
| C、2x+y-4=0 |
| D、2x+y+4=0 |
考点：直线的截距式方程
专题：直线与圆
分析：由已知条件设直线l的方程为：
+
=1，化简单整理后能求出直线l的斜率k，由此能求出直线l的方程．
| x |
| k |
| y |
| 2k |
解答：
解：∵直线l的斜率为k（k≠0），
它在x轴、y轴上的截距分别为k、2k，
∴设直线l的方程为：
+
=1，
整理，得2x+y=2k，
∴k=-2，
∴直线l的方程为：2x+y=-4，
即2x+y+4=0．
故选D．
它在x轴、y轴上的截距分别为k、2k，
∴设直线l的方程为：
| x |
| k |
| y |
| 2k |
整理，得2x+y=2k，
∴k=-2，
∴直线l的方程为：2x+y=-4，
即2x+y+4=0．
故选D．
点评：本题考查直线的截距式方程的求法，是基础题，解题时要注意直线斜率的灵活运用．
练习册系列答案
阅读快车系列答案
相关题目
已知集合A={x|x＞-2}．且A∪B=A，则集合B可以是（ ）
| A、{x|x2＞4} | ||
B、{x|y=
| ||
| C、{y|y=x2-2，x∈R} | ||
| D、{-1，0，1，2，3} |
以初速度40m/s竖直向上抛一物体，t秒时刻的速度v=40-10t2，则此物体达到最高时的高度为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若不论m取何实数，直线l：mx+y-1+2m=0恒过一定点，则该定点的坐标为（ ）
| A、（-2，1） |
| B、（2，-1） |
| C、（-2，-1） |
| D、（2，1） |
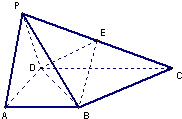如图，四棱锥P-ABCD的底面ABCD为一直角梯形，侧面PAD是等边三角形，其中BA⊥AD，CD⊥AD，CD=2AD=2AB，平面PAD⊥底面ABCD，E是PC的中点．函数f（x）=x2+14x-3在区间（-5，5）上最大值、最小值情况为（ ）
| A、有最大值，没最小值 |
| B、有最小值，没最大值 |
| C、有最大值，也有最小值 |
| D、没有最大值，也没有最小值 |