题目内容
【选修4-5:不等式选讲】
已知不等式x+|3x-3|<5的解集为M.
(Ⅰ)求集合M;
(Ⅱ)若a,b∈M,证明:ab-2<2b-a.
已知不等式x+|3x-3|<5的解集为M.
(Ⅰ)求集合M;
(Ⅱ)若a,b∈M,证明:ab-2<2b-a.
考点:绝对值不等式的解法
专题:不等式的解法及应用,不等式
分析:(Ⅰ)利用绝对值的意义:不等式x+|3x-3|<5可化为
或
解得即可.
(Ⅱ)由于a,b∈M,可得(ab-2)-(2b-a)=(ab+a)-(2b+2)=(b+1)(a-2)<0即可证明.
|
|
(Ⅱ)由于a,b∈M,可得(ab-2)-(2b-a)=(ab+a)-(2b+2)=(b+1)(a-2)<0即可证明.
解答:
证明:(Ⅰ) 不等式x+|3x-3|<5可化为
或
解得-1<x≤1或1<x<2)
∴M=(-1,2).
(Ⅱ)∵a,b∈M,∴-1<a<2,-1<b<2.
∴(ab-2)-(2b-a)=(ab+a)-(2b+2)=(b+1)(a-2)<0
∴ab-2<2b-a.
|
|
解得-1<x≤1或1<x<2)
∴M=(-1,2).
(Ⅱ)∵a,b∈M,∴-1<a<2,-1<b<2.
∴(ab-2)-(2b-a)=(ab+a)-(2b+2)=(b+1)(a-2)<0
∴ab-2<2b-a.
点评:本题考查了含绝对值的不等式的解法、分类讨论、元素与集合的关系、“作差法”证明不等式等基础知识与基本技能方法,属于中档题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
函数f(x)=x2+14x-3在区间(-5,5)上最大值、最小值情况为( )
| A、有最大值,没最小值 |
| B、有最小值,没最大值 |
| C、有最大值,也有最小值 |
| D、没有最大值,也没有最小值 |
在△ABC中,A=60°,a=4
,b=4
,则B=( )
| 3 |
| 2 |
| A、30° | B、45° |
| C、120° | D、135° |
直线2x-3y+1=0和x-3=0的夹角是( )
A、π-arctan
| ||||
B、
| ||||
C、arctan
| ||||
D、
|
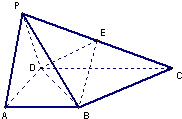 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB,平面PAD⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB,平面PAD⊥底面ABCD,E是PC的中点.