Question

1．已知集合M={（x，y）|y=f（x）}，若对任意p₁（x₁，y₁）∈M，均存在p₂（x₂，y₂）∈M，使得x₁x₂+y₁y₂=0成立，则称集合M为“优越集”，给出下列集合：
①M=$\left\{{（x，y）\left|{y=\frac{1}{x}}\right.}\right\}$
②M={（x，y）|y=lnx}
③M={（x，y）|y=-x²+1}
④M={（x，y）|（x-2）²+y²=1}
⑤M={（x，y）|x²-2y²=1}
其中所有“优越集”的序号是②③．

Answer 1

分析 根据“优越集”的定义逐个验证即可得到答案．

解答 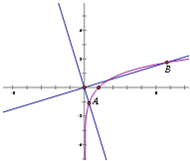解：x₁x₂+y₁y₂=0⇒$\overrightarrow{O{P}_{1}}⊥\overrightarrow{O{P}_{2}}$，（O为坐标原点），即OP₁⊥OP₂．若集合M里存在两个元素P₁，P₂，使得OP₁⊥OP₂，
则集合M是“优越集”，否则不是．
对于①：任意两点与原点连线夹角小于90°或大于90°，
集合M里不存在两个元素P₁，P₂，使得OP₁⊥OP₂，
则集合M不是“优越集”；
对于②：如图，函数y=lnx的图象上存在两点A，B，使得OA⊥OB．所以M是“优越集”；
对于③：函数的图象上存在两点A（0，1），B（1，0），使得OA⊥OB．所以M是“优越集”；
对于④：切线方程为y=±$\frac{\sqrt{3}}{3}$x，夹角为60°，集合M里不存在两个元素P₁，P₂，使得OP₁⊥OP₂，则集合M不是“优越集”；
对于⑤：双曲线x²-2y²=1的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x，两条渐近线的夹角小于90°，集合M里不存在两个元素P₁，P₂，使得OP₁⊥OP₂，则集合M不是“优越集”，
故答案为：②③．

点评 本题考查了命题真假的判断与应用，考查了元素与集合的关系，考查了数形结合的思想，解答的关键是对新定义的理解，是中档题．