题目内容
1.已知tanα=2且$π<α<\frac{3π}{2}$,则sinα的值是-$\frac{2\sqrt{5}}{5}$.分析 利用三角函数基本关系式即可得出.
解答 解:∵tanα=2且$π<α<\frac{3π}{2}$,则sinα<0.
∴$\frac{sinα}{cosα}$=2,sin2α+cos2α=1,
联立解得sinα=-$\frac{2\sqrt{5}}{5}$.
故答案为:-$\frac{2\sqrt{5}}{5}$.
点评 本题考查了三角函数基本关系式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
11.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为( )
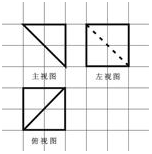

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
12.已知奇函数f(x)满足,x>0时,f(x)=x2-2x;则x<0时,f(x)的解析式为( )
| A. | -x2-2x | B. | -x2+2x | C. | x2-2x | D. | x2+2x |
13.函数$f(x)=tan(ωx+\frac{π}{3})(ω>0)$的最小正周期为$\frac{π}{2}$,为了得到y=tanωx的图象,只需把y=f(x)的图象上所有点( )
| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{12}$个长度单位 |
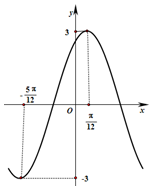 函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为y=3sin(2x+$\frac{π}{3}$).
函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为y=3sin(2x+$\frac{π}{3}$).