题目内容
过原点的椭圆的一个焦点为F(1,0),其长轴长为4,则椭圆中心的轨迹方程是( )
A、(x-
| ||||
B、(x+
| ||||
C、x2+(y-
| ||||
D、x2+(y+
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设中心坐标P(x,y),据已知的一个焦点和P可以推出另外一个焦点,再根据椭圆性质列方程:O到F,F'的距离之和=2a通过化简即可求出结果.
解答:
解:∵长轴长为4,∴2a=4,
设椭圆中心P(x,y),另外一个焦点的坐标就是F'(2x-1,2y)
据椭圆的定义:
+
=2a=4
整理得:
(2x-1)2+4y2=9
即:(x-
)2+y2=
故椭圆中心的轨迹方程为:(x-
)2+y2=
故选:A
设椭圆中心P(x,y),另外一个焦点的坐标就是F'(2x-1,2y)
据椭圆的定义:
| (0-1)2+(0-0)2 |
| (0+1-2x)2+(0-2y)2 |
整理得:
(2x-1)2+4y2=9
即:(x-
| 1 |
| 2 |
| 9 |
| 4 |
故椭圆中心的轨迹方程为:(x-
| 1 |
| 2 |
| 9 |
| 4 |
故选:A
点评:本题考查椭圆轨迹方程问题,通过已知椭圆的性质和公式,设出中心坐标然后利用已知等式化简求结果.本题属于难题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
函数f(x)=e
的定义域是( )
| x2-1 |
| A、[-1,1] |
| B、[1,+∞) |
| C、(-∞,-1] |
| D、(-∞,-1]∪[1,+∞) |
根据如下数据:
得到回归方程为
=bx+a,则ab的值( )
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| ∧ |
| y |
| A、大于0 | B、等于0 |
| C、小于0 | D、不能确定 |
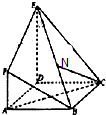 如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DF∥AF,AB=DE=2,AF=1.
如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DF∥AF,AB=DE=2,AF=1.