题目内容
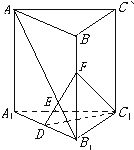如图，直三棱柱ABC-A1B1C1中，已知AC=BC=AA1=a，∠ACB=90°，D是A1B1中点．（1）求证：C1D⊥平面A1B1BA；
（2）请问，当点F在BB1上什么位置时，会使得AB1⊥平面C1DF？并证明你的结论．
考点：直线与平面垂直的判定,直线与平面垂直的性质
专题：空间位置关系与距离
分析：（1）根据AC=BC，判断出△ABC为等腰三角形，又A1D=DB1，知C1D⊥A1B1，最后利用线面垂直的判定定理推断出C1D⊥平面A1B1BA
（2）由（1）可得：C1D⊥AB1，又要使AB1⊥平面C1DF，只要DF⊥AB1即可，又∠ACB=∠A1C1B1=90°，且AC=BC=AA1=a，求得A1B1=
a，由△AA1B1∽△DB1F，推断出
=
，进而可知B1F=a即当：F点与B点重合时，会使AB1⊥平面C1DF．
（2）由（1）可得：C1D⊥AB1，又要使AB1⊥平面C1DF，只要DF⊥AB1即可，又∠ACB=∠A1C1B1=90°，且AC=BC=AA1=a，求得A1B1=
| 2 |
| AA1 |
| DB1 |
| A1B1 |
| B1F |
解答：
解：（1）∵AC=BC，
∴△ABC为等腰三角形，
又∵A1D=DB1，
∴C1D⊥A1B1，
∵C1D⊥A1A，AA1∩A1B1=A1，
∴C1D⊥平面A1B1BA
（2）由（1）可得：C1D⊥AB1，
又要使AB1⊥平面C1DF，只要DF⊥AB1即可，
又∵∠ACB=∠A1C1B1=90°，且AC=BC=AA1=a，
∴A1B1=
a，
∵△AA1B1∽△DB1F，
∴
=
，
∴B1F=a
即当：F点与B点重合时，会使AB1⊥平面C1DF．
∴△ABC为等腰三角形，
又∵A1D=DB1，
∴C1D⊥A1B1，
∵C1D⊥A1A，AA1∩A1B1=A1，
∴C1D⊥平面A1B1BA
（2）由（1）可得：C1D⊥AB1，
又要使AB1⊥平面C1DF，只要DF⊥AB1即可，
又∵∠ACB=∠A1C1B1=90°，且AC=BC=AA1=a，
∴A1B1=
| 2 |
∵△AA1B1∽△DB1F，
∴
| AA1 |
| DB1 |
| A1B1 |
| B1F |
∴B1F=a
即当：F点与B点重合时，会使AB1⊥平面C1DF．
点评：本题主要考查了线面垂直的判定定理．考查了学生分析和推理的能力．
练习册系列答案
相关题目
已知集合A={x|x2+2x-3≤0}，B={x|x2≤4}，则A∩B=（ ）
| A、{x|-2≤x≤1} |
| B、{x|0≤x≤1} |
| C、{x|-3≤x≤2} |
| D、{x|1≤x≤2} |
在线段[0，3]上任取一点，则此点坐标不大于1的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|