题目内容
已知函数f(x)=alnx+
x2-(1+a)x.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若f(x)≥0对定义域内的任意x恒成立,求实数a的取值范围;
(Ⅲ)证明:对于任意不小于2的正整数n,不等式
+
…+
>1-
恒成立.
| 1 |
| 2 |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若f(x)≥0对定义域内的任意x恒成立,求实数a的取值范围;
(Ⅲ)证明:对于任意不小于2的正整数n,不等式
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| lnn |
| 1 |
| n |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)先求出函数f(x)的导数,通过讨论a的取值范围得出函数的单调区间;
(Ⅱ)由于f(1)=-
-a,显然当a>0时,f(1)<0,此时f(x)≥0对定义域每的任意x不是恒成立的,当a≤0时,根据(1)得出即可;
(Ⅲ)当a=-
时,f(x)=-
lnx+
x2-
x≥0,等号当且仅当x=1成立,这个不等式即lnx≤x2-x,再将不等式变形即可证出.
(Ⅱ)由于f(1)=-
| 1 |
| 2 |
(Ⅲ)当a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵f′(x)=
+x-(1+a)=
=
.
(Ⅰ)当a≤0时,若0<x<1,则f'(x)<0,若x>1,则f'(x)>0,故此时函数f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞);
当0<a<1时,f'(x),f(x)的变化情况如下表:
所以函数f(x)的单调递增区间是(0,a),(1,+∞),单调递减区间是(a,1);
当a=1时,f′(x)=
≥0,函数f(x)的单调递增区间是(0,+∞);
当a>1时,同0<a<1可得,函数f(x)的单调递增区间是(0,1),(a,+∞),
单调递减区间是(1,a).
(Ⅱ)由于f(1)=-
-a,显然当a>0时,f(1)<0,此时f(x)≥0对定义域每的任意x不是恒成立的,
当a≤0时,根据(1),函数f(x)在区间(0,+∞)的极小值、也是最小值即是f(1)=-
-a,
此时只要f(1)≥0即可,解得a≤-
,故得实数a的取值范围是(-∞,-
].
(Ⅲ)当a=-
时,f(x)=-
lnx+
x2-
x≥0,等号当且仅当x=1成立,
这个不等式即lnx≤x2-x,当x>1时,可以变换为
>
=
,
在上面不等式中分别令x=2,3,4…,n,
+
…+
>
+
+…+
=1-
∴
+
…+
>1-
.
| a |
| x |
| x2-(1+a)x+a |
| x |
| (x-1)(x-a) |
| x |
(Ⅰ)当a≤0时,若0<x<1,则f'(x)<0,若x>1,则f'(x)>0,故此时函数f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞);
当0<a<1时,f'(x),f(x)的变化情况如下表:
| x | (0,a) | a | (a,1) | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
当a=1时,f′(x)=
| (x-1)2 |
| x |
当a>1时,同0<a<1可得,函数f(x)的单调递增区间是(0,1),(a,+∞),
单调递减区间是(1,a).
(Ⅱ)由于f(1)=-
| 1 |
| 2 |
当a≤0时,根据(1),函数f(x)在区间(0,+∞)的极小值、也是最小值即是f(1)=-
| 1 |
| 2 |
此时只要f(1)≥0即可,解得a≤-
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ)当a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
这个不等式即lnx≤x2-x,当x>1时,可以变换为
| 1 |
| lnx |
| 1 |
| x2-x |
| 1 |
| (x-1)x |
在上面不等式中分别令x=2,3,4…,n,
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| lnn |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)n |
| 1 |
| n |
∴
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| lnn |
| 1 |
| n |
点评:本题考察了函数的单调性,利用导数求函数的单调区间,求参数的取值范围,以及不等式的证明,本题是一道综合题.

练习册系列答案
相关题目
已知f(x)=
,则f(
)的值为( )
| sin(π-x)•cos(2π-x) |
| cos(-π-x)•tan(π-x) |
| π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
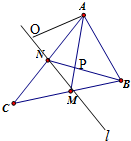 在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设
在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设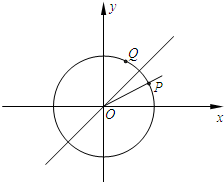 如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.
如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.