题目内容

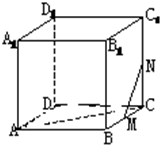在正方体ABCD-A1B1C1D1中，求证：
（1）平面A1BD∥平面CB1D1；
（2）M、N分别为棱BC和棱CC1的中点，求异面直线AC和MN所成的角．
考点：平面与平面平行的判定,异面直线及其所成的角
专题：空间位置关系与距离,空间角
分析：（1）连接 B1C和 D1C，由A1D∥B1C，A1B∥D1C，能证明平面CB1D1∥平面A1BD．
（2）利用正方体的性质容易得到AD1∥MN，所以∠CAD1为异面直线所成的角，连接CD1，得到△CAD1为等边三角形，得到所求．
解答： （1）证明：连接 B1C和 D1C，
∵A1D∥B1C，A1B∥D1C，
A1D∩A1B=A1，
A1D?平面A1BD，A1B?平面A1BD，
B1C?平面CB1D1，D1C?平面CB1D1，
∴平面A1BD∥平面CB1D1．
（2）解：因为几何体为正方体，连接AD1，D1C，所以∠CAD1为异面直线所成的角，
又△CAD1为等边三角形，
所以异面直线AC和MN所成的角60°
点评：本题考查两平面平行的证明，考查异面直线所成的角的求法，关键是将面面平行转化为线线平行解答，将空间角转化为平面角解答，注意转化能力和空间思维能力的培养．
练习册系列答案
相关题目
求函数y=2sin2x的单调递增区间．
tan（-
17π
6
）=（　　）
A、
3
B、-
3
C、-
3
3
D、
3
3
下列命题中，正确的是
 

（1）曲线y=lnx在点（1，0）处的切线方程是y=x-1；
（2）函数y=
16-2x
的值域是[0，4]；
（3）已知
a
=(sinθ，
1+cosθ
)，
b
=(1，
1-cosθ
)，其中θ∈(π，
3π
2
)，则
a
⊥
b
；
（4）O是△ABC所在平面上一定点，动点P满足：
OP
=
OA
+λ(
AB
sinC
+
AC
sinC
)，λ∈（0，+∞），则直线1过三角形的内心．
如图1，⊙O的直径AB=4，点C，D为⊙O上任意两点，∠CAB=45°，∠DAB=60°，F为
BC
的中点，沿直径AB折起，使两个半圆所在平面互相垂直．
（1）求证：OF∥面ACD；
（2）求二面角A-CD-B的大小．
已知数列{an}（n∈N*），其前n项和为Sn，给出下列四个命题：
①若{an}是等差数列，则三点(10，
S10
10
)、(100，
S100
100
)、(110，
S110
110
)共线；
②若{an}是等差数列，且a1=-11，a3+a7=-6，则S1、S2、…、Sn这n个数中必然存在一个最大者；
③若{an}是等比数列，则Sm、S2m-Sm、S3m-S2m（m∈N*）也是等比数列；
④若Sn+1=a1+qSn（其中常数a1q≠0），则{an}是等比数列；
⑤若等比数列{an}的公比是q（q是常数），且a1=1，则数列{an2}的前n项和sn=
1-q2n
1-q2
．
其中正确命题的序号是
 
．（将你认为正确命题的序号都填上）
已知a，b表示直线，α，β表示平面，下列推理正确的是（　　）
A、α∩β=a，b?α⇒a∥b
B、α∩β=a，a∥b⇒b∥α且b∥β
C、a∥β，b∥β，a?α，b?α⇒α∥β
D、α∥β，α∩γ=a，β∩γ=b⇒a∥b
如图是一个几何体的三视图，则该几何体的体积是
 
．
用min{a，b，c}表示a，b，c三个数中的最小值，设f（x）=min{2x，x+1，10-x}（x≥0），则f（x）的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网