题目内容
下列命题中,正确的是
(1)曲线y=lnx在点(1,0)处的切线方程是y=x-1;
(2)函数y=
的值域是[0,4];
(3)已知
=(sinθ,
),
=(1,
),其中θ∈(π,
),则
⊥
;
(4)O是△ABC所在平面上一定点,动点P满足:
=
+λ(
+
),λ∈(0,+∞),则直线1过三角形的内心.
(1)曲线y=lnx在点(1,0)处的切线方程是y=x-1;
(2)函数y=
| 16-2x |
(3)已知
| a |
| 1+cosθ |
| b |
| 1-cosθ |
| 3π |
| 2 |
| a |
| b |
(4)O是△ABC所在平面上一定点,动点P满足:
| OP |
| OA |
| ||
| sinC |
| ||
| sinC |
考点:命题的真假判断与应用
专题:平面向量及应用,简易逻辑
分析:(1)直接利用导数求得切线方程判断(1);
(2)由指数函数的值域求得无理函数的值域判断(2);
(3)利用平面向量的数量积运算结合同角三角函数的基本关系式判断(3);
(4)由平面向量的几何意义分析(4).
(2)由指数函数的值域求得无理函数的值域判断(2);
(3)利用平面向量的数量积运算结合同角三角函数的基本关系式判断(3);
(4)由平面向量的几何意义分析(4).
解答:
解:对于(1),由y=lnx,得y′=
,则y′|x=1=1,曲线在点(1,0)处的切线方程是y=x-1,命题正确;
对于(2),∵2x>0,∴-2x<0,
∴函数y=
的值域是[0,4),命题错误;
对于(3),已知
=(sinθ,
),
=(1,
),其中θ∈(π,
),则
•
=sinθ+
=sinθ-sinθ=0,
∴
⊥
,命题正确;
对于(4),O是△ABC所在平面上一定点,动点P满足:
=
+λ(
+
),λ∈(0,+∞),
则
=
+2Rλ(
+
),
∵
,
分别表示
,
方向上的单位向量,
∴
+
的方向与∠BAC的角平分线一致,
∵
=
+2Rλ(
+
),
∴
=2Rλ(
+
),
∴
的方向与∠BAC的角平分线一致,
则直线1一定通过三角形的内心,命题正确.
故答案为:(1)(3)(4).
| 1 |
| x |
对于(2),∵2x>0,∴-2x<0,
∴函数y=
| 16-2x |
对于(3),已知
| a |
| 1+cosθ |
| b |
| 1-cosθ |
| 3π |
| 2 |
| a |
| b |
| 1-cos2θ |
∴
| a |
| b |
对于(4),O是△ABC所在平面上一定点,动点P满足:
| OP |
| OA |
| ||
| sinC |
| ||
| sinC |
则
| OP |
| OA |
| ||
|
|
| ||
|
|
∵
| ||
|
|
| ||
|
|
| AB |
| AC |
∴
| ||
|
|
| ||
|
|
∵
| OP |
| OA |
| ||
|
|
| ||
|
|
∴
| AP |
| ||
|
|
| ||
|
|
∴
| AP |
则直线1一定通过三角形的内心,命题正确.
故答案为:(1)(3)(4).
点评:本题考查了命题的真假判断与应用,考查了平面向量的数量积运算,训练了平面向量的应用,是中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
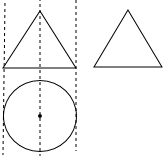 如图,一个空间几何体的正视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的内切球表面积为( )
如图,一个空间几何体的正视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的内切球表面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=
+x的图象可能是( )
| |x| |
| x |
A、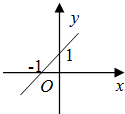 |
B、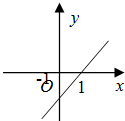 |
C、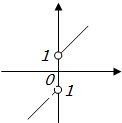 |
D、 |
已知二次函数y=x2+mx+4,当x∈R时,恒有y>0,则m的取值范围是( )
| A、(0,2) |
| B、(-2,2) |
| C、(-4.4) |
| D、(-2,0) |
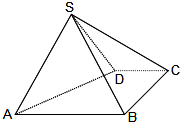 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=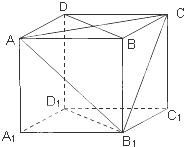 如图,在棱长为1的正方体ABCD-A1B1C1D1中.
如图,在棱长为1的正方体ABCD-A1B1C1D1中.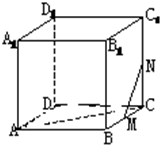 在正方体ABCD-A1B1C1D1中,求证:
在正方体ABCD-A1B1C1D1中,求证: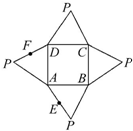 如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论: