题目内容
求函数y=2sin2x的单调递增区间．
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：直接利用正弦函数的单调区间整体代入即可求出结论．
解答：
解：因为函数y=2sin2x；
令2kπ-
≤2x≤2kπ+
⇒kπ-
≤x≤kπ+
（k∈Z）．
所以函数y=sin2x的单调递增区间：[kπ-
，kπ+
]，k∈Z．
令2kπ-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
所以函数y=sin2x的单调递增区间：[kπ-
| π |
| 4 |
| π |
| 4 |
点评：本题主要考查正弦函数的单调性以及整体代入思想，一般再解三角函数的单调区间时，多用整体代入思想来解决．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
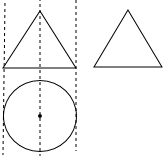如图，一个空间几何体的正视图和左视图都是边长为1的正三角形，俯视图是一个圆，那么这个几何体的内切球表面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=x-sin2x的图象为（ ）
A、 |
B、 |
C、 |
D、 |
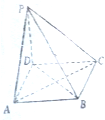如图，在四棱锥P-ABCD中，底面是边长为a的正方形，侧棱PD=a，PA=PC=
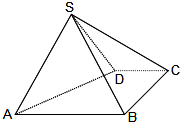如图，四棱锥S-ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形．AB=BC=2，CD=1，SD=
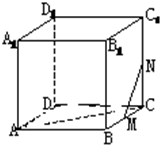在正方体ABCD-A1B1C1D1中，求证：