题目内容
 如图1,⊙O的直径AB=4,点C,D为⊙O上任意两点,∠CAB=45°,∠DAB=60°,F为
如图1,⊙O的直径AB=4,点C,D为⊙O上任意两点,∠CAB=45°,∠DAB=60°,F为 |
| BC |
(1)求证:OF∥面ACD;
(2)求二面角A-CD-B的大小.
考点:用空间向量求平面间的夹角
专题:空间位置关系与距离
分析:(1)只要证明OF∥AC即可;
(2)过O作OE⊥AD于点E,连接CE,∠CEO是二面角C-AD-B的平面角,然后求之.
(2)过O作OE⊥AD于点E,连接CE,∠CEO是二面角C-AD-B的平面角,然后求之.
解答:
解:(1)连接CO,∵∠CAB=45°,OA=OC,∴CO⊥AB,又∵F为
的中点,∴∠FOB=45°,
∴OF∥AC,
∵OF?平面ACD,AC?平面ACD,
∴OF∥平面ACD.
(2)过O作OE⊥AD于点E,连接CE,
∵CO⊥AB,平面ABC⊥平面ABD,
∴CO⊥平面ABD,
又∵AD?平面ABD,
∴CO⊥AD,∴AD⊥平面CEO,∴AD⊥CE,
则∠CEO是二面角C-AD-B的平面角
∵∠OAD=60°,OA=2,∴OE=
,
由CO⊥平面ABD,OE?平面ABD,得△CEO为直角三角形,
∵CO=1,∴CE=
,∴cos∠CEO=
=
.
所以∠CEO=arccos
.
 |
| BC |
∴OF∥AC,
∵OF?平面ACD,AC?平面ACD,
∴OF∥平面ACD.
(2)过O作OE⊥AD于点E,连接CE,
∵CO⊥AB,平面ABC⊥平面ABD,
∴CO⊥平面ABD,
又∵AD?平面ABD,
∴CO⊥AD,∴AD⊥平面CEO,∴AD⊥CE,
则∠CEO是二面角C-AD-B的平面角
∵∠OAD=60°,OA=2,∴OE=
| 3 |
由CO⊥平面ABD,OE?平面ABD,得△CEO为直角三角形,
∵CO=1,∴CE=
| 7 |
| ||
|
| ||
| 7 |
所以∠CEO=arccos
| ||
| 7 |
点评:本题考查了线面平行的判定和二面角的平面角的求法,关键是将所求转化为线线平行、平面角解答,属于中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
设点D,E分别在△ABC的边BC,AC上,线段AD,BE相交于点F,则“F为△ABC的重心”是“
=
=2”的( )
| AF |
| FD |
| BF |
| FE |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |

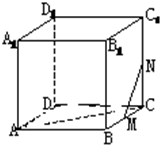 在正方体ABCD-A1B1C1D1中,求证:
在正方体ABCD-A1B1C1D1中,求证: 已知正三棱锥S-ABC内接于半径为4的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如下,则此三棱锥的体积为
已知正三棱锥S-ABC内接于半径为4的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如下,则此三棱锥的体积为