题目内容
已知：如图三角形ABC中，AB=AC，∠A=36°，∠1=∠2，AE=EB，ED交BC于F，求证：AC2=BC•BF．考点：相似三角形的判定
专题：选作题,立体几何
分析：证明△ABC∽△FAB，即可证明结论．
解答：
证明：因为△ABC中，AB=AC，∠A=36°所以∠ABC=∠ACB=72°
因为∠1=∠2，所以∠1=∠2=36°=∠A
所以AD=DB，
因为AE=EB，ED交BC于F，
所以EF垂直平分AB，
所以AF=BF，
所以△ABC∽△FAB，
∴
=
，
因为AB=AC，
所以AC2=BC•BF．
证明：因为△ABC中，AB=AC，∠A=36°所以∠ABC=∠ACB=72°因为∠1=∠2，所以∠1=∠2=36°=∠A
所以AD=DB，
因为AE=EB，ED交BC于F，
所以EF垂直平分AB，
所以AF=BF，
所以△ABC∽△FAB，
∴
| AC |
| BF |
| BC |
| AB |
因为AB=AC，
所以AC2=BC•BF．
点评：本题考查相似三角形的判定，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
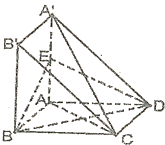如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，AA′⊥平面ABCD