题目内容
已知函数f(x)=ax2-2bx+a(a,b∈R),若a从集合{0,1,2}中任取一个元素,b从集合{0,1,2,3}中任取一个元素,求方程f(x)=0恰有两个不相等实根的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:根据已知计算出a从集合{0,1,2}中任取一个元素,b从集合{0,1,2,3}中任取一个元素的方法总数,和方程f(x)=0恰有两个不相等实根的方法种数,代入古典概型概率计算公式,可得答案.
解答:
解:a从集合{0,1,2}中任取一个元素,b从集合{0,1,2,3}中任取一个元素,
共有:3×4=12种不同的取法,
若方程f(x)=0恰有两个不相等实根,
即△=4b2-4a2>0,即b>a共有:
(0,1),(0,2),(0,3),
(1,2),(1,3),(2,3)共6种,
故方程f(x)=0恰有两个不相等实根的概率P=
=
.
共有:3×4=12种不同的取法,
若方程f(x)=0恰有两个不相等实根,
即△=4b2-4a2>0,即b>a共有:
(0,1),(0,2),(0,3),
(1,2),(1,3),(2,3)共6种,
故方程f(x)=0恰有两个不相等实根的概率P=
| 6 |
| 12 |
| 1 |
| 2 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
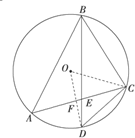 如图,⊙O是△ABC的外接圆,D是
如图,⊙O是△ABC的外接圆,D是 
 已知:如图三角形ABC中,AB=AC,∠A=36°,∠1=∠2,AE=EB,ED交BC于F,求证:AC2=BC•BF.
已知:如图三角形ABC中,AB=AC,∠A=36°,∠1=∠2,AE=EB,ED交BC于F,求证:AC2=BC•BF.