题目内容
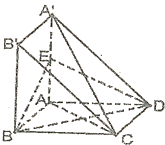如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，AA′⊥平面ABCD（1）求证：A′C∥平面BDE；
（2）求证：平面A′AC⊥平面BDE．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）首先找到线面平行的充分条件，可以通过中位线找到线线平行，再进一步证明线面平行．
（2）要证明平面A′AC⊥平面BDE．可以通过BD⊥平面A'AC来进行转化，进一步找到BD⊥平面A'AC的充分条件，从而得到结果．
（2）要证明平面A′AC⊥平面BDE．可以通过BD⊥平面A'AC来进行转化，进一步找到BD⊥平面A'AC的充分条件，从而得到结果．
解答：
证明：（1）设BD交AC于M，连结ME．
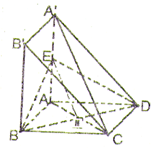
∵ABCD为正方形，所以M为AC中点，
又∵E为A'A的中点∴ME为△A'AC的中位线
∴ME∥A'C又∵ME?平面BDE，A'C?平面BDE
∴A'C∥平面BDE．
（2）∵ABCD为正方形
∴BD⊥AC
∵A'A⊥平面ABCD∴A'A⊥BD．
又AC∩A'A=A AC?面A'AC AA'?面A'AC
∴BD⊥平面A'AC
∵BD?平面BDE
∴平面A'AC⊥平面BDE．
∵ABCD为正方形，所以M为AC中点，
又∵E为A'A的中点∴ME为△A'AC的中位线
∴ME∥A'C又∵ME?平面BDE，A'C?平面BDE
∴A'C∥平面BDE．
（2）∵ABCD为正方形
∴BD⊥AC
∵A'A⊥平面ABCD∴A'A⊥BD．
又AC∩A'A=A AC?面A'AC AA'?面A'AC
∴BD⊥平面A'AC
∵BD?平面BDE
∴平面A'AC⊥平面BDE．
点评：本题考查的知识点：三角形的中位线，线面平行的判定定理，线面垂直的性质定理，线面垂直的判定定理，面面垂直的判定定理．是高考的重点题型．
练习册系列答案
相关题目
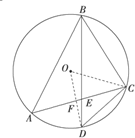如图，⊙O是△ABC的外接圆，D是 
已知：如图三角形ABC中，AB=AC，∠A=36°，∠1=∠2，AE=EB，ED交BC于F，求证：AC2=BC•BF．