题目内容
4.已知$\overrightarrow{m}$=(2$\sqrt{3}$,1),$\overrightarrow{n}$=(cos2$\frac{A}{2}$,sinA),A,B,C是△ABC的内角.(1)当A∈(0,$\frac{π}{2}$)时,求|$\overrightarrow{n}$|的取值范围;
(2)若C=$\frac{2π}{3}$,AB=3,当$\overrightarrow{m}$•$\overrightarrow{n}$取最大值时,求A的大小及边BC的长.
分析 (1)当A∈(0,$\frac{π}{2}$)时,|$\overrightarrow{n}$|2=($\frac{1+cosA}{2}$)2+sin2A=$-\frac{3}{4}(cosA-\frac{1}{3})^{2}$+$\frac{1}{3}$,即可求|$\overrightarrow{n}$|的取值范围;
(2)$\overrightarrow{m}$•$\overrightarrow{n}$=2$\sqrt{3}$cos2$\frac{A}{2}$+sinA=$\sqrt{3}$cosA+sinA+$\sqrt{3}$=2sin(A+$\frac{π}{3}$)+$\sqrt{3}$,当A+$\frac{π}{3}$=$\frac{π}{2}$,即A=$\frac{π}{6}$时,$\overrightarrow{m}$•$\overrightarrow{n}$取最大值,利用正弦定理求出边BC的长.
解答 解:(1)$\overrightarrow{n}$=(cos2$\frac{A}{2}$,sinA)=($\frac{1+cosA}{2}$,sinA),
∴|$\overrightarrow{n}$|2=($\frac{1+cosA}{2}$)2+sin2A=$-\frac{3}{4}(cosA-\frac{1}{3})^{2}$+$\frac{1}{3}$,
∵A∈(0,$\frac{π}{2}$),∴cosA∈(0,1),
∴|$\overrightarrow{n}$|的取值范围是(0,$\frac{\sqrt{3}}{3}$];
(2)$\overrightarrow{m}$•$\overrightarrow{n}$=2$\sqrt{3}$cos2$\frac{A}{2}$+sinA=$\sqrt{3}$cosA+sinA+$\sqrt{3}$=2sin(A+$\frac{π}{3}$)+$\sqrt{3}$,
∵A∈(0,$\frac{π}{2}$),∴A+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{5π}{6}$),
∴A+$\frac{π}{3}$=$\frac{π}{2}$,即A=$\frac{π}{6}$时,$\overrightarrow{m}$•$\overrightarrow{n}$取最大值2+$\sqrt{3}$,
由正弦定理可得$\frac{BC}{sin\frac{π}{6}}$=$\frac{3}{sin\frac{2π}{3}}$,∴BC=$\sqrt{3}$.
点评 本题考查向量知识的运用,考查三角函数知识的运用,考查正弦定理,属于中档题.

| A. | 在区间($\frac{1}{e}$,1),(1,e)内均有零点 | |
| B. | 在区间($\frac{1}{e}$,1),(1,e)内均无零点 | |
| C. | 在区间($\frac{1}{e}$,1)内有零点,在区间(1,e内无零点 | |
| D. | 在区间($\frac{1}{e}$,1)内无零点,在区间(1,e)内有零点 |
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7 | 6 | 5 | 4 | 2 |
(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
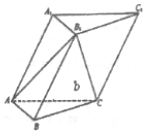 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC.