题目内容
5.函数$y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$在同一个周期内,当x=$\frac{π}{4}$时y取最大值2,当x=$\frac{7π}{12}$时,y取最小值-2.(1)求函数的解析式y=f(x).
(2)若x∈[0,2π],且f(x)=$\sqrt{3}$时,求x的值;
(3)若函数f(x)满足方程f(x)=a(1<a<2),求在[0,2π]内的所有实数根之和.
分析 (1)由函数的最值可得A,再根据周期求得ω,再由五点法作图求得φ,可得函数的解析式.
(2)根据正弦函数的性质可得3x-$\frac{π}{4}$=2kπ+$\frac{π}{3}$,或3x-$\frac{π}{4}$=2kπ+$\frac{2π}{3}$,问题得以解决,
(3)若函数f(x)满足方程f(x)=a(1<a<2),则在[0,2π]内方程f(x)=a有6个根,即可求出答案
解答 解:(1)由函数的最值可得A=2,再根据$\frac{1}{2}$T=$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{4}$,求得ω=3.
再由五点法作图可得 3×$\frac{π}{4}$+φ=$\frac{π}{2}$,∴φ=-$\frac{π}{4}$,故函数的解析式y=f(x)=2sin(3x-$\frac{π}{4}$).
(2)∵x∈[0,2π],且f(x)=$\sqrt{3}$时,
∴2sin(3x-$\frac{π}{4}$)=$\sqrt{3}$,
∴3x-$\frac{π}{4}$=2kπ+$\frac{π}{3}$,或3x-$\frac{π}{4}$=2kπ+$\frac{2π}{3}$,
∴x=$\frac{2}{3}$kπ+$\frac{7π}{36}$或x=$\frac{2}{3}$kπ+$\frac{11π}{36}$,
当k=0时,x=$\frac{7π}{36}$或$\frac{11π}{36}$,
当k=1时,x=$\frac{31π}{36}$或$\frac{35π}{36}$,
当k=2时,x=$\frac{55π}{36}$或$\frac{59π}{36}$,
(3)若函数f(x)满足方程f(x)=a(1<a<2),
则在[0,2π]内方程f(x)=a有6个根,
∴x1+x2=$\frac{π}{2}$,x3+x4=$\frac{π}{2}$+$\frac{4}{3}$π,x5+x6=$\frac{π}{2}$+$\frac{8}{3}$π,
∴和为$\frac{3π}{2}$+4π=$\frac{11}{2}$π.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的图象和性质,属于中档题

| A. | 若a,b∈R且a+b=1,则a•b≤$\frac{1}{4}$ | |
| B. | 若a,b∈R,则$\frac{{a}^{2}+{b}^{2}}{2}$≥($\frac{a+b}{2}$)2≥ab恒成立 | |
| C. | $\frac{{x}^{2}+3}{\sqrt{{x}^{2}+1}}$ (x∈R) 的最小值是2$\sqrt{2}$ | |
| D. | x0,y0∈R,x02+y02+x0y0<0 |
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7 | 6 | 5 | 4 | 2 |
(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
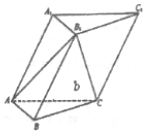 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC.