题目内容
在△ABC中,已知a,b,c为它的三边,且△ABC的面积为
,则角C= .
| a2+b2-c2 |
| 4 |
考点:余弦定理
专题:解三角形
分析:由已知和余弦定理可得sinC=cosC,即tanC=1,即可解得C的值.
解答:
解:S△ABC=
,即
absinC=
,
∴sinC=
,
∵由余弦定理知:cosC=
,
∴sinC=cosC,即tanC=1,
∵C为三角形的内角,
∴C=45°,
故答案为:45°.
| a2+b2-c2 |
| 4 |
| 1 |
| 2 |
| a2+b2-c2 |
| 4 |
∴sinC=
| a2+b2-c2 |
| 2ab |
∵由余弦定理知:cosC=
| a2+b2-c2 |
| 2ab |
∴sinC=cosC,即tanC=1,
∵C为三角形的内角,
∴C=45°,
故答案为:45°.
点评:本题主要考察了余弦定理的应用,属于基础题.

练习册系列答案
相关题目
下面的程序运行的功能是( )


A、求1+
| ||||||
B、求1+
| ||||||
C、求1+1+
| ||||||
D、求1+1+
|
设x2+y2+z2=1,若λxyz≤
对一切x,y,z∈R*均成立,则λ的最大值为( )
| 1+z |
| 2 |
A、2(
| ||||
B、
| ||||
| C、4 | ||||
| D、3 |
已知双曲线C的方程为
-
=1(a,b>0),其离心率为e,直线l与双曲线C交于A、B两点,线段AB中点M在第一象限,并且在抛物线y2=2px(p>0)上,且M到抛物线焦点距离为p,则直线l的斜率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、e 2-1 | ||
C、
| ||
| D、e 2+1 |
设x∈R,向量
=(x,1),
=(1,-2),且
⊥
,则|
+
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、2
| ||
D、
|
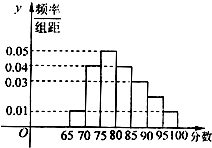 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.