题目内容
10．设集合A={-2，-1，0，1，2}，B={x|x2+2x＜0}，则A∩B=（ ）| A． | {1，2} | B． | {-2，-1} | C． | {-1} | D． | {-2，-1，0} |
分析 化简集合B，根据交集的定义写出A∩B即可．
解答 解：集合A={-2，-1，0，1，2}，
B={x|x2+2x＜0}={x|-2＜x＜0}，
则A∩B={-1}．
故选：C．
点评 本题考查了集合的化简与运算问题，是基础题目．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
20．
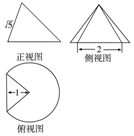一个圆锥被过顶点的平面截去了较小的一部分，余下的几何体的三视图如图，则该几何体的体积为（ ）
一个圆锥被过顶点的平面截去了较小的一部分，余下的几何体的三视图如图，则该几何体的体积为（ ）| A． | $π+\frac{2}{3}$ | B． | $π+\frac{1}{3}$ | C． | $\frac{3}{4}π+\frac{2}{3}$ | D． | $\frac{3}{4}π+\frac{1}{3}$ |
18．已知点（x，y）满足不等式组$\left\{\begin{array}{l}x-y+3≥0\\ 2x-y-1≤0\\ 3x+2y-6≥0\end{array}\right.$，则$z=\frac{y}{x+1}$的最小值为（ ）
| A． | 3 | B． | $\frac{7}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{7}{5}$ |
5．等差数列{an}中，若a3+a6+a9=12，则数列{an}的前11项和等于（ ）
| A． | 22 | B． | 33 | C． | 44 | D． | 55 |
15．若$sinθcosθ=\frac{1}{2}$，则$tanθ-\frac{cosθ}{sinθ}$的值是（ ）
| A． | -2 | B． | 0 | C． | ±2 | D． | $\frac{1}{2}$ |
2．双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$的渐近线所在直线方程为（ ）
| A． | $x=±\frac{{\sqrt{3}}}{3}y$ | B． | $y=±\frac{{\sqrt{3}}}{3}x$ | C． | $y=±\frac{{\sqrt{3}}}{2}x$ | D． | $x=±\frac{{\sqrt{3}}}{2}y$ |