题目内容
19.已知函数f(x)=x-alnx-$\frac{b}{x}-2({a,b∈{R}})$.(Ⅰ)当a-b=1,a>1时,讨论函数f(x)的单调性;
(Ⅱ)当b=-1,a≤4时,不等式f(x)<-$\frac{3}{x}$在区间[2,4]上恒成立,求实数a的取值范围.
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)问题转化为$x-alnx+\frac{4}{x}-2<0$,令$g(x)=x-alnx+\frac{4}{x}-2$,求出函数g(x)的导数,通过讨论a的范围确定函数的单调性确定a的范围即可.
解答 解:(Ⅰ)由题知x∈(0,+∞),
∵$f'(x)=1-\frac{a}{x}+\frac{b}{x^2}$,且由a-b=1得b=a-1,
∴$f'(x)=1-\frac{a}{x}+\frac{b}{x^2}=\frac{{{x^2}-ax+a-1}}{x^2}=\frac{{({x-1})({x-a+1})}}{x^2}$,
当a-1=1即a=2时,$f'(x)=\frac{{{{({x-1})}^2}}}{x^2}≥0$,
知函数f(x)的单调增区间为(0,+∞);
当a-1>1即a>2时,知x∈(0,1)和x∈(a-1,+∞)时f'(x)>0,
当x∈(1,a-1)时,f'(x)<0
故函数f(x)的单调增区间(0,a-1)和(1,+∞),单调减区间为(a-1,1);
综上所述,当a=2时,函数f(x)的单调增区间为(0,+∞);
当a>2时,函数f(x)的单调增区间(0,1)和(a-1,+∞),单调减区间为(1,a-1);
当1<a<2时,故函数f(x)的单调增区间(0,a-1)和(1,+∞),单调减区间为(a-1,1)
(Ⅱ)当b=-1时$f(x)=x-alnx+\frac{1}{x}-2$,由$f(x)<-\frac{3}{x}$得$x-alnx+\frac{4}{x}-2<0$,
令$g(x)=x-alnx+\frac{4}{x}-2$,则$g'(x)=1-\frac{a}{x}-\frac{4}{x^2}=\frac{{{x^2}-ax-4}}{x^2}$
设$t={x^2}-ax-4={({x-\frac{a}{2}})^2}-4-\frac{a^2}{4}$,由a≤4知对称轴$x=\frac{a}{2}≤2$,
故t=x2-ax-4在[2,4]上单调递增,
所以当x=2时,tmin=-2a,当x=4时,tmax=12-4a,
①当12-4a≤0,即3≤a≤4时,g'(x)≤0,知g(x)在[2,4]上单调递减,
得$a>\frac{2}{ln2}$,故3≤a≤4.
②当-2a≥0,即a≤0时,g'(x)≥0,知g(x)在[2,4]上单调递增,
g(x)max=g(4)=3-aln4<0,得$a>\frac{3}{ln4}$,故此时无解.
③当-2a<0<12-4a,即0<a<3时,
g'(x)=0在(2,4)上有唯一一个实数解x0,
且g(x)在x∈(2,x0)上单调递减,在x∈(x0,4)上单调递增,
要使g(x)<0恒成立,
只需$\left\{\begin{array}{l}g(2)<0\\ g(4)<0\end{array}\right.⇒\left\{\begin{array}{l}a>\frac{2}{ln2}\\ a>\frac{3}{ln4}\end{array}\right.$,得$a>\frac{2}{ln2}$,故$\frac{2}{ln2}<a<3$.
综上①②③知$\frac{2}{ln2}<a≤4$,
所以实数a的取值范围为$({\frac{2}{ln2},4}]$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案| A. | y=3x | B. | y=x2 | C. | y=lnx | D. | y=x|x| |
| A. | {1,2} | B. | {-2,-1} | C. | {-1} | D. | {-2,-1,0} |
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | 若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | B. | f(x)的图象关于点($\frac{π}{12}$,0)对称 | ||
| C. | f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | f(x)在区间(-$\frac{π}{3}$,$\frac{π}{12}$)上是增函数 |
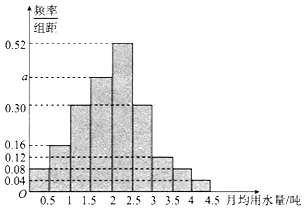 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.