题目内容
15.若$sinθcosθ=\frac{1}{2}$,则$tanθ-\frac{cosθ}{sinθ}$的值是( )| A. | -2 | B. | 0 | C. | ±2 | D. | $\frac{1}{2}$ |
分析 由已知利用二倍角正弦求得sin2θ=1,cos2θ=0,再化切为弦,通分后求得$tanθ-\frac{cosθ}{sinθ}$的值.
解答 解:∵$sinθcosθ=\frac{1}{2}$,
∴$\frac{1}{2}sin2θ=\frac{1}{2}$,则sin2θ=1,∴cos2θ=0.
∴$tanθ-\frac{cosθ}{sinθ}$=$\frac{sinθ}{cosθ}-\frac{cosθ}{sinθ}=\frac{si{n}^{2}θ-co{s}^{2}θ}{sinθcosθ}$
=$\frac{si{n}^{2}θ-co{s}^{2}θ}{\frac{1}{2}}=-2cos2θ$=0.
故选:B.
点评 本题考查三角函数的化简求值,考查倍角公式的应用,是基础的计算题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.已知集合M={x|-1≤x<3,x∈R},N={-1,0,1,2,3},则M∩N=( )
| A. | {-1,0,2,3} | B. | {-1,0,1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
6.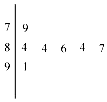 某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
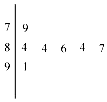 某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,4 | D. | 85,1.6 |
10.设集合A={-2,-1,0,1,2},B={x|x2+2x<0},则A∩B=( )
| A. | {1,2} | B. | {-2,-1} | C. | {-1} | D. | {-2,-1,0} |
20.如图是某几何体的三视图,则该几何体的体积为( )


| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
4.已知复数z=a+i,a∈R,若z+$\overline{z}$=2,则复数z的共轭复数$\overline{z}$=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
5.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺.大鼠日自倍,小鼠日自半.问几何日相逢?各穿几何?”,翻译成今天的话是:一只大鼠和一只小鼠分别从的墙两侧面对面打洞,已知第一天两鼠都打了一尺长的洞,以后大鼠每天打的洞长是前一天的2倍,小鼠每天打的洞长是前一天的一半,已知墙厚五尺,问两鼠几天后相见?相见时各打了几尺长的洞?设两鼠x 天后相遇(假设两鼠每天的速度是匀速的),则x=( )
| A. | $2\frac{1}{18}$ | B. | $2\frac{1}{17}$ | C. | $2\frac{2}{17}$ | D. | $2\frac{1}{9}$ |
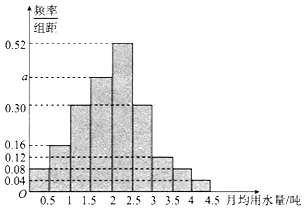 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.