题目内容
3.记[x]表示不超过实数x的最大整数.设集合A={(x,y)|x2+y2≤1},B={(x,y)|[x]2+[y]2≤1}.则A∪B所表示的平面区域的面积为5+$\frac{π}{4}$.分析 讨论x∈[-1,0)与x∈[0,1)和x∈[1,2)时,化简集合B,求出A∪B所表示的平面区域所对应的面积.
解答 解:集合A表示一个以原点(0,0)为圆心的单位圆(即半径为1的圆);
集合B可以这样考虑:当x∈[-1,0)时,[x]=-1,于是[y]=0,y∈[0,1);
当x∈[0,1)时,[x]=0,于是[y]=-1或0或1,y∈[-1,2);
当x∈[1,2)时,[x]=1,于是[y]=0,y∈[0,1);
画出图形,如图所示;
所以A∪B所表示的平面区域由五个单位正方形和第三象限的$\frac{1}{4}$单位圆构成,
其面积为$5+\frac{π}{4}$.
故答案为:5+$\frac{π}{4}$.
点评 本题考查了不等式表示平面区域的应用问题,也考查了分类讨论思想的应用问题,是基础题目.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
18.已知向量$\overrightarrow p=(2,-3)$,$\overrightarrow q=(x,6)$,且$\overrightarrow p$∥$\overrightarrow q$,则$|{\overrightarrow p+\overrightarrow q}|$的值为( )
| A. | 13 | B. | 14 | C. | $\sqrt{13}$ | D. | $\sqrt{14}$ |
12.如图,A,B,C,D是平面上的任意四点,下列式子中正确的是( )
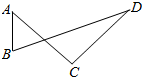

| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{BC}$+$\overrightarrow{DA}$ | B. | $\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{AD}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{DB}$=$\overrightarrow{DC}$+$\overrightarrow{BA}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{DA}$=$\overrightarrow{AC}$+$\overrightarrow{DB}$ |
 如图,OA是南北方向的一条公路,OB是北偏东45°方向的一条公路,某风景区的一段边界为曲线C.为方便游客光,拟过曲线C上的某点分别修建与公路OA,OB垂直的两条道路PM,PN,且PM,PN的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy,则曲线符合函数y=x+$\frac{{4\sqrt{2}}}{x^2}$(1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.
如图,OA是南北方向的一条公路,OB是北偏东45°方向的一条公路,某风景区的一段边界为曲线C.为方便游客光,拟过曲线C上的某点分别修建与公路OA,OB垂直的两条道路PM,PN,且PM,PN的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy,则曲线符合函数y=x+$\frac{{4\sqrt{2}}}{x^2}$(1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.