题目内容
7.若${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中所有项系数的绝对值之和为1024,则该展开式中的常数项是( )| A. | -270 | B. | 270 | C. | -90 | D. | 90 |
分析 ${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中所有项系数的绝对值之和等于$(\frac{3}{\sqrt{x}}+\root{3}{x})^{n}$为展开式中所有项系数的绝对值之和,令x=1可得:4n=1024,解得n=5.利用$(\frac{3}{\sqrt{x}}-\root{3}{x})^{5}$的通项公式即可得出.
解答 解:${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中所有项系数的绝对值之和等于$(\frac{3}{\sqrt{x}}+\root{3}{x})^{n}$为展开式中所有项系数的绝对值之和,
令x=1可得:4n=1024,解得n=5.
∴$(\frac{3}{\sqrt{x}}-\root{3}{x})^{5}$的通项公式为:Tr+1=${∁}_{5}^{r}(\frac{3}{\sqrt{x}})^{5-r}(-\root{3}{x})^{r}$=(-1)r${∁}_{5}^{r}$35-r${x}^{\frac{5r-15}{6}}$,
令$\frac{5r-15}{6}$=0,解得r=3.
∴该展开式中的常数项是$(-1)^{3}{∁}_{5}^{3}×{3}^{2}$=-90.
故选:C.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
2.设A,B是两个非空集合,定义集合A-B={x|x∈A且x∉B}.若A={x∈N|0≤x≤5},B={x|x2-7x+10<0},则A-B=( )
| A. | {0,1} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,5} |
19.在正数数列{an}中,a1=2,且点$(a_n^2,a_{n-1}^2)$在直线x-9y=0上,则{an}的前n项和Sn等于( )
| A. | 3n-1 | B. | $\frac{{1-{{({-3})}^n}}}{2}$ | C. | $\frac{{1+{3^n}}}{2}$ | D. | $\frac{{3{n^2}+n}}{2}$ |
17.已知函数f(x)=log3|x-t|是偶函数,记$a=f({{{log}_{0.3}}4}),b=f({{π^{1.5}}}),c=f({2-t})$则a,b,c的大小关系为( )
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |
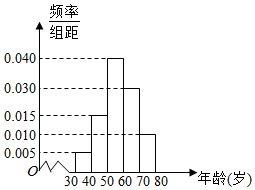 某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.
某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.