题目内容
17.已知函数f(x)=log3|x-t|是偶函数,记$a=f({{{log}_{0.3}}4}),b=f({{π^{1.5}}}),c=f({2-t})$则a,b,c的大小关系为( )| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |
分析 由f(x)为偶函数,可得t=0,讨论x>0时,f(x)递增,化a=f(log0.30.25),运用指数函数和对数函数的单调性,比较π1.5、2、log0.30.25的大小,即可得到a,b,c的大小关系.
解答 解:函数f(x)=log3|x-t|是偶函数,
可得f(-x)=f(x),即log3|-x-t|=log3|x-t|,
即有|-x-t|=|x-t|恒成立,可得t=0,
则f(x)=log3|x|,当x>0时,f(x)=log3x为增函数,
a=f(log0.34)=f(log0.30.25),c=f(2-t)=f(2),
由1<log0.30.25<2,π1.5>π>3,
即有π1.5>2>log0.30.25,
则f(π1.5)>f(2)>f(log0.30.25),
即为b>c>a.
故选:A.
点评 本题考查函数的奇偶性和单调性的判断和应用:比较大小,注意运用定义法和转化思想,同时考查指数函数和对数函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
7.若${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中所有项系数的绝对值之和为1024,则该展开式中的常数项是( )
| A. | -270 | B. | 270 | C. | -90 | D. | 90 |
8.对于函数f(x)=atanx+bx3+cx(a、b、c∈R),选取a、b、c的一组值计算f(1)、f(-1),所得出的正确结果可能是( )
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
12.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的一个焦点与抛物线${y^2}=4\sqrt{3}x$的焦点重合,长轴长等于圆x2+y2-2x-15=0的半径,则椭圆C的方程为( )
| A. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
6.若复数z 满足z(1+i)=-2i(i为虚数单位),则复数z 在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知函数f(x)=$\left\{\begin{array}{l}{10x-1,x≤0}\\{{e}^{x},x>0}\end{array}\right.$(e为自然对数的底).若函数g(x)=f(x)-kx恰好有两个零点,则实数k的取值范围是( )
| A. | (1,e) | B. | (e,10] | C. | (1,10] | D. | (10,+∞) |
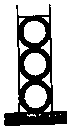 圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.
圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.