题目内容
复数z=
(i是虚数单位)的共轭复数
在复平面内对应的点在( )
| i |
| 1-i |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则、共轭复数的意义、复数的几何意义即可得出.
解答:
解:∵复数z=
=
=
=-
+
i,
∴z共轭复数
=-
-
i在复平面内对应的点为(-
,-
)在第三象限.
故选:C.
| i |
| 1-i |
| i(1+i) |
| (1-i)(1+i) |
| -1+i |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴z共轭复数
. |
| z |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题考查了复数的运算法则、共轭复数的意义、复数的几何意义,属于基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
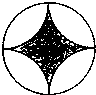 如图,将半径为l的圆分成相等的四段弧,再将四段弧围成星形放在圆内(阴影部分).现在往圆内任投一点,此点落在星形区域内的概率为( )
如图,将半径为l的圆分成相等的四段弧,再将四段弧围成星形放在圆内(阴影部分).现在往圆内任投一点,此点落在星形区域内的概率为( )A、
| ||||
B、
| ||||
C、1-
| ||||
D、
|
设x,y满足约束条件
,则目标函数z=x+2y的最大值是( )
|
| A、3 | B、4 | C、5 | D、6 |
甲、乙、丙、丁、戊共5人站成一排,其中甲、乙两人中间恰有1人的站法种数是( )
| A、18 | B、24 | C、36 | D、48 |
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )


| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
已知函数f(x)=sin(
-x),若要得到函数f′(x)的图象,只需将函数y=f(x)图象上所有的点( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|